1. 粒子示踪微流变学
通过将微米/纳米尺寸的粒子添加到复杂流体介质中并监测它们的热运动,我们可以获得有关该复杂流体线性粘弹性的定量信息。与传统流变测量方法相比,该技术主要应用于空间受限条件下的少量样品。这类新技术称为微流变学1,具体又分为主动和被动两类。在主动微流变学中,粒子受实验者操纵。粒子的位移和作用在粒子上的力被换算为为介质流体的应力和应变。在被动微流变学中,粒子可以自由地进行热运动。我们基于广义朗之万方程和广义流体动力学,从粒子位移的统计数据中获得介质流体的线性粘弹性。我们主要进行被动微流变学研究,但也非常关注主动微流变学领域的发展。
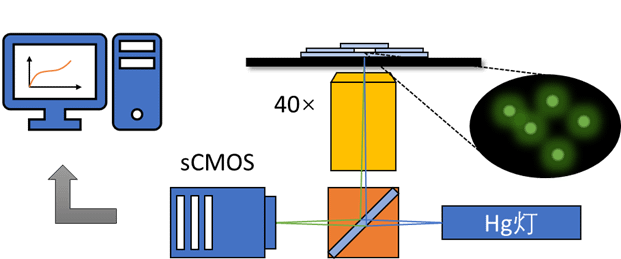
按照被动微流变学的一般方法学,具体实验实施方式是多种多样的。 在我们的实验室中,我们使用荧光显微镜结合 sCMOS 相机来获取预先悬浮在复杂流体中的荧光标记粒子的延时视频。 接下来,我们使用图像处理技术从视频中提取粒子的轨迹数据。 然后,基于对粒子轨迹的统计分析,得到有关介质流体的物理信息。 我们的研究实现了复杂流体的以下两种物理信息的测量,使被动微流变学成为软物质研究中的独特而强大的方法。
1.1 尺度依赖的粘度
连续介质的粘度不仅具有时间尺度依赖性(即粘弹性),还具有空间尺度依赖性2,3。这样的粘度称为广义粘度。在傅立叶域,广义粘度依赖频率和波矢。粘度的尺度依赖性由流体本构关系的记忆函数表征。对于时间尺度依赖性,传统上常采用流变仪测量,但这对应于在空间尺度无穷大(零波矢)极限。只有当检测的空间尺度与被测流体的结构或动力学相关长度相当时,才能观察到粘度的空间尺度依赖性。这一尺度范围对复杂流体而言是从几纳米到微米。基于胶体粒子的广义流体动力学理论,我们可以方便地测量这种长度尺度依赖性,而无需首先为样品创建足够小的空间限制,因为粘度的空间尺度依赖性与测量结果的表观粒径依赖性或“斯托克斯-爱因斯坦破缺”是定量相关的。
1.2 动力学不均匀性的空间尺度
动力学不均匀性是液体密度涨落的时空相关性4。在粒子示踪微流变学中,液体的动力学不均匀性间接地导致粒子热运动的非高斯统计特征。我们提出了一种微流变学分析框架,通过系统地比较单粒子和多粒子统计数据,可从粒子的统计数据中定量地提取出液体的动力学不均匀性空间尺度。这一方法已成功应用在凝胶化体系的研究中。
2. 软物质的液固转变
我们将软物质理解为由介观的“结构单元”通过弱相互作用直接组成的宏观系统。这种定义下的例子包括聚合物、胶体、乳液、泡沫等。 软物质的共同特性是它们的表观固/液状态对时间尺度的依赖性(即粘弹性)以及它们机械响应中明显的非线性。因此,软物质的“固体”和“液体”只有一些模糊的定义,从而导致“软物质的液固转变”的定义更加模糊。
我们重新考虑了软物质的固体和液体的概念,并基于软物质的粘弹性谱提出了一种液固转变的的现象学分类方式。这启发将启法人们进一步将液固转变表观类型与不同化学或分子成分软物质体系之间液固转变的共性物理机制建立联系。
3. 新型水凝胶的物理化学
在过去的几十年里,通过将优异的机械强度于与刺激响应特性结合一身,水凝胶的应用领域得到了重要的开拓,例如软驱动器、可穿戴/可植入传感器和机器人等。 构建这些新型水凝胶的策略涉及复杂的化学、热力学和流变学过程,其理论基础尚未完全奠定。
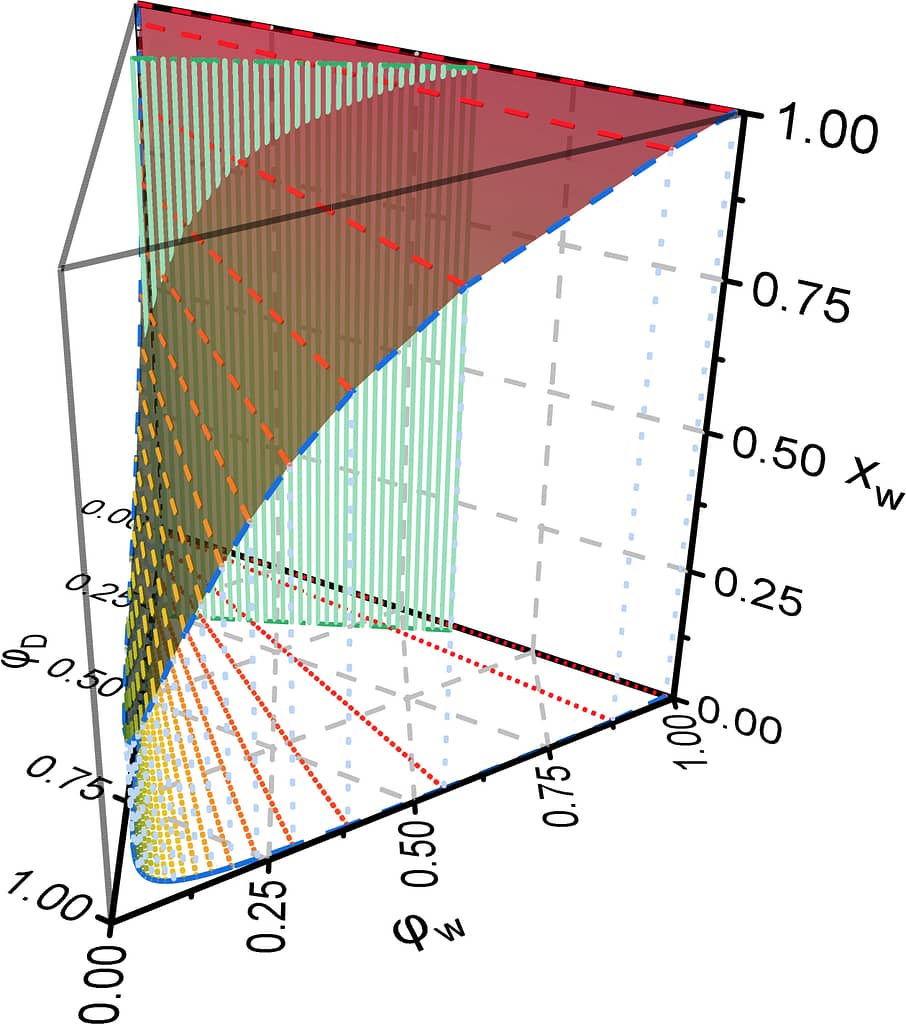
我们特别关注由聚合物网络、溶剂和非溶剂组成的模型体系。我们通过理论和实验相结合的方法,研究这些体系的相分离、玻璃化转变和力学性能之间的基本理论。 我们的研究为新型水凝胶材料的理性工程设计和工业应用提供了必须的理论模型。
参考文献
- (1)Waigh, T. A. Advances in the Microrheology of Complex Fluids. Reports on Progress in Physics 2016, 79 (7), 074601. https://doi.org/10.1088/0034-4885/79/7/074601.
- (2)Evans, D. J.; Morriss, G. Statistical Mechanics of Nonequilibrium Liquids, 2nd ed.; Cambridge University Press: Cambridge, 2008. https://doi.org/DOI: 10.1017/CBO9780511535307.
- (3)Generalized Hydrodynamics. Physics Today 1984, 37 (1), 56–63. https://doi.org/10.1063/1.2916048.
- (4)Berthier, L.; Biroli, G.; Bouchaud, J.-P.; Cipelletti, L.; van Saarloos, W. Dynamical Heterogeneities in Glasses, Colloids, and Granular Media; Oxford University Press: Oxford, 2011. https://doi.org/10.1093/acprof:oso/9780199691470.001.0001.