1. Particle tracking microrheology

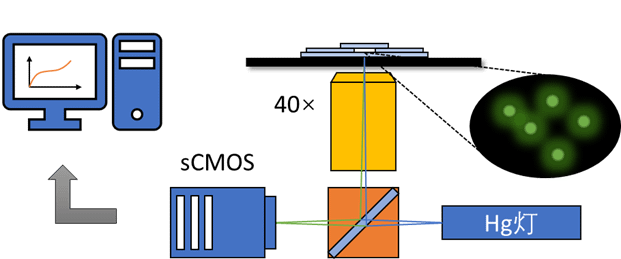
By adding micro-/nanometer-sized particles into a medium of complex fluid and monitoring their thermal motions, we can gain quantitative information about the linear viscoelasticity of that complex fluid. This technique is mostly applied to small amount of sample in a spatially confined condition compared with the case of traditional rheometry. This class of new techniques are called microrheology^​1​, which is subdivided into active and passive one. In the active microrheology, the particles are manipulated by the experimenter in a controlled manner. The displacements of, and the forces acted on the particle are converted into the stress and strain of the medium fluid. We do not perform active microrheological experiments but are highly aware of the development of this field. In the passive microrheology, on the other hand, the particles are left freely for thermal motions. The linear viscoelasticity of the medium fluid is obtained from the statistics of the particle displacements based on generalized Langevin equation and generalized hydrodynamics. We do research on passive microrheology.

There are a large variety of experimental implementation under the general methodology of passive microrheology. In our lab, we used fluorescent microscope combined with an sCMOS camera to acquire time-lapse videos of fluorescence-labeled particles pre-suspended in a complex fluid. Next, we use image processing technique (improved based on reported routine) to extract trajectory data of the particles from the videos. Then, multi-particle trajectories are analyzed based on developed theories, providing different physical insight about the medium fluids. Among many, our study enables the following two aspects of physical information of complex fluids that make passive microrheology a unique and powerful approach in soft matter research.

1.1 The length-scale dependent viscosity

Viscosity of continua is not only time-dependent, as in the case of viscoelasticity, but also length-scale dependent, to an extent that fades as distance of two points increases^​2,3​. The spatiotemporal Fourier domain counterpart of this generalized viscosity is accordingly frequency and wave-vector dependent. The effect of time-dependence viscosity is characterized by the memory function of the constitutive relation of the fluid, which can be measured by traditional rheometers, but at the limit of infinite length-scale (zero wave vector). Finite length-scale dependence is observable only when the detecting length scale is comparable to the structural or dynamic correlation length of the fluid, which ranges from several nanometers to microns for complex fluids. The hydrodynamics of colloidal particles in a complex fluid allow the measurement of such a length-scale dependence without the trouble of creating small enough confinement for the sample in the first place; instead, the length-scale dependent of the viscosity is quantitatively related to the apparent particle-size dependent or “Stokes–Einstein breakdown” of the measured results.

1.2 The length scale of dynamic heterogeneity

Dynamic heterogeneity is the spatiotemporal correlation in the density fluctuation of a fluid^​4​. Under particle tracking microrheology, dynamic heterogeneity of the fluid causes non-Gaussian statistics of the particles. We have proposed a framework to further extract the length-scale of the former from the data of the latter, by systematically comparing single-particle and multi-particle statistics. The success of this technique has been demonstrated in our published research on systems undergoing sol-gel transition.

2. The liquid-to-solid transition of soft matter

We are particularly interested in the physics of the liquid-to-solid transition of soft matter. We understand soft matter as macroscopic systems that are composed directly of large, mesoscopic “building blocks” via weak interactions. Examples under such definition include polymers, colloids, emulsions, foams, etc. The common property of soft matter is the dependence of their apparent solid/liquid states on timescale (i.e., again, viscoelasticity) as well as the obvious nonlinearity in their mechanical response. Therefore, there is only some murky definition of “solid” and “liquid” for soft matter, which leads to an even murkier definition of “liquid-to-solid transition”.

We reconsidered the concept of solid and liquid for soft matter and proposed a phenomenological categorization of liquid-to-solid transition based on the viscoelastic spectrum of soft matter. This creates heuristics to further relate the apparent category of the transition to the generality of the underneath physics across systems of different detailed chemical or molecular components.

3. Physical chemistry of new hydrogels

In the past decades, the combination of mechanical strength with stimuli-responsive property in hydrogel materials have opened a new horizon of application of hydrogels, e.g., soft actuators, wearable/implantable sensors, and robots. Strategies of constructing these advanced hydrogels involve complications in chemical, thermodynamic, and rheological processes the theoretical basis of which is not completely laid.

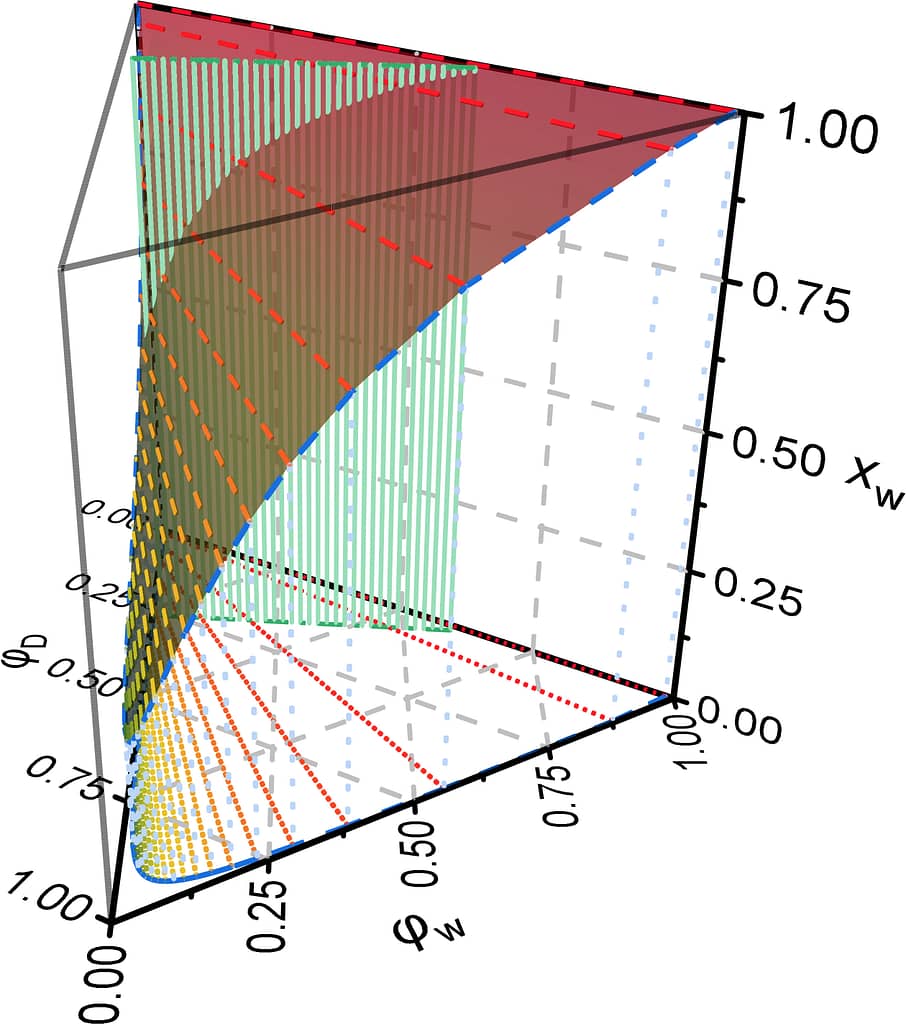
We are particularly concerned with the model systems consisting of a polymer network, a solvent, and a non-solvent. The interplay among phase separation, glass transition, and the mechanical property of these systems is investigated in a combined approach of theory and experiment. Our research provides models and laws for rational and engineered design of new hydrogel materials.