函数的平移叠加性是怎么来的？

最近写paper，所以基本上没时间在博客上长篇大论。倒是自从开通中文微博之后由于无需切换翻墙代理因此基本上长年挂在上面。现在如果你想挂微博，基本上什么客户端都有了。在所有各种手机，各种操作系统。但我发现，只有使用Chrome插件客户端之后我才真正利用了客户端实现长挂。这说明我的工作中心是Chrome浏览器。

WordPress升及到3.2之后也顺眼了N多，主要是Dashboard用的font family好像清理过了，该sans的sans、该serif的serif，就连monospaced的也很好看。在使用一段时间微博之后，发现这还是属于不假思索的人用的。所以基本上我还是会回归博客。

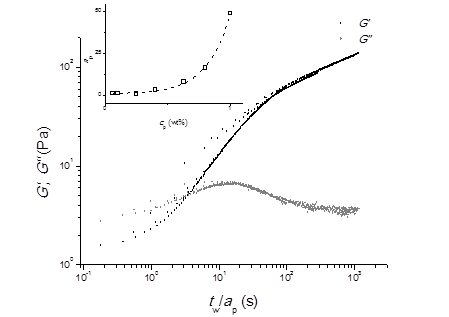
我的paper涉及到一个凝胶化过程的时间浓度叠加性，既不同浓度的体系凝胶化曲线（测的是模量曲线）log-log图可以通过水平平移叠加成一条主曲线的现象。我需要说明的是这时的平移因子就是凝胶化反应速率常数k。这好像本来是个显而易见的道理，但我发现一下子没办法清晰的说清楚，不得不查文献。渐渐发现以上事实的前提只需要是“单分子反应”即可。即只要是在谈论单分子反应，不管是几级反应。如果反应过程具有时间叠加性，那么平移因子就是速率常数。以下是通过简单的推导来展示这一事实。

Master curve and the shift factor

Master curve and the shift factor

一个n级单分子反应速率方程是：

\frac{d \left[ A \right]}{dt}=k\left[ A\right]^{n}

积分之后就是：

\begin{cases}& \left[A \right ]=\left[A\right]_{0}\exp\left(-kt\right),n=1\\ & \left[A \right ]=\left[\left(n-1 \right )kt+\left[A \right ]_{0}^{1-n}\right]^{\frac{1}{1-n}},n\neq1 \end{cases}

可见，速率方程总可以直接写成t'=kt的函数：\left[A\right]=f\left(t\right)=f\left(kt\right)。这时，如果k对某参量C（如浓度）有依赖性，并可以写成k=k_{0} a_{C}\left(C\right)，则有 f\left( kt /a_{C}\right)\equiv f\left(k_{0} t\right)，即f\left(t'/a_{C}\right) \equiv f\left(t_{0}'\right)。作成log-log图，则为\lg f\left(\lg t'-\lg a_{C}\right)\equiv\lg f\left(\lg t_{0}'\right)，即具有平移叠加等效性。

同理，关于结晶的过程有个Avrami方程X=\exp\left(-kt^n\right)。此时X能写成t'=kt^n的单值函数：X=X\left(t'\right)=\exp\left(-t'\right)。这时，如果结晶的速率常数k是温度的函数并可以写成：k=k_{0}a_{T}，那么就有f\left(t'/a_{T}\right) \equiv f\left(t_{0}'\right)、\lg f\left(\lg t'-\lg a_{T}\right) \equiv \lg f\left(\lg t_{0}'\right)，其log-log图同样具有平移叠加等效性。