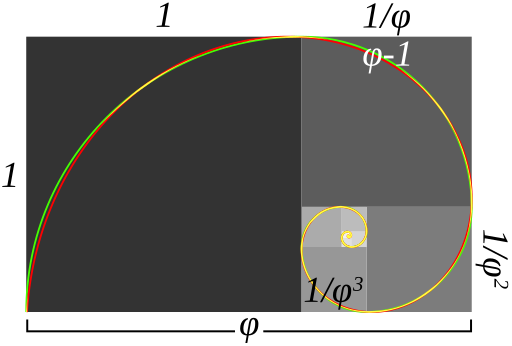
黄金比例数大家都知道,是一个无理数$\phi=1.618\cdots$。许多理论论证大自然很多自发或最优的结果遵循这个比例,美术、建筑和音乐上这个比例也产生了神奇的和谐。利用这个比例可作出黄金螺线。
上图是三种形状十分接近黄金螺线的螺线。
最近在网上看到另一个类似的无理数,叫“塑料数”(plastic number)。我觉得比较有趣的是,把音符按按似黄金比例的Fibonacci数列排列,发现是经常被使用的旋律1,2,3,5,这个梗已经广为人所知。那么用plastic number作比例的Padovan数列得出的旋律是怎么样的呢?这篇文章探讨了这个问题。
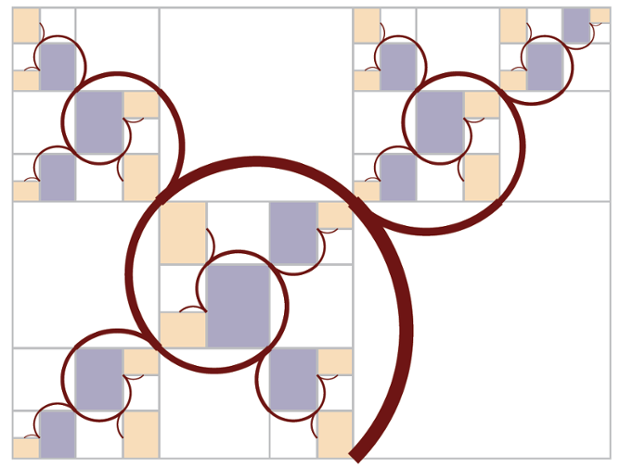
跟Fibonacci数列不同,Padovan数列得到的螺线,是会分叉的,于是能够形成十分美丽的花纹。这是由一个热爱螺线的数学家发现的。英国《卫报》报道过他的发现。文末他说,他还考察过其他特殊比例数,但没有得到像plastic number这样美丽的图案。
这种花纹乍一看会感觉像某棵植物。植物中出线螺线的情况确实很多,还有个术语叫“叶序”(Phyllotaxis)。一定叶序的形成是有机制的。一定机制产生螺旋的情况在大自然中很常见,这篇博客还有更多的例子。
在Wikipedia上能够找到很多种数学上的螺线。
- Golden spiral
- Logarithmic spiral
- Archimedean spiral
- Hyperbolic spiral
- Rose
- Fermat’s spiral
- Spiral of Theodorus
现在,由plastic number产生的螺线,以发现他的数学家Edmund Harriss命名为Harris spiral,这个spiral是分叉的。按照plastic number还能构建三维的螺线。