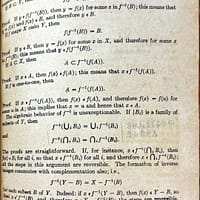虽然我远没有看完Paul Richard Halmos(1916~2006)的所有数学教材,但我确实看了几本话题比较大众化的——因而同类教材也比较多的——从而在比较的基础上可以支撑我对Halmos的偏爱。所以我仍然能够直接说,我特别喜欢Halmos的数学书。
我看过他写的集合论、测度论、有限维向量空间和希尔伯特空间。这些书除了测度论之外都是很薄的。
至少我还不完整地看过他的自传——I want to be a mathematician。这个自传的开头就先明确地反醒了作者的人格特质,读来发现与我本人十分贴近,这足以支持我偏爱他的著作。这段话对其他读者来说也可以说明Halmos很可能是总能写出好教材的数学家。
I like words more than numbers, and I always did.
Then why, you might well ask, am I a mathematician? I don’t know. I can see some of the reasons in the story of my life, and I can see that chance played a role at least as big as choice; I’ll try to tell about all that as we go along. I do know that I wasn’t always sure what I wanted to be.
The sentence I began with explains the way I feel about a lot of things, and how I got that way. It implies, for instance, or in any event I men for it to imply that in mathematics I like the conceptual more than the computational. To me the definition of a group is far clearer and more important and more beautiful than the Cauchy integral formula. Is it unfair to compare a concept with a fact? Very well, to me the infinite differentiability of a once differentiable complex function is far superior in beauty and depth to the celebrated Campbell–Baker–Hausdorff formula about non-commutative exponentiation.
The beginning sentence includes also the statement that I like to understand mathematics, and to clarify it for myself and for the world, more even than to discover it. The joy of suddenly learning a former secret and the joy of suddenly discovering a hitherto unknown truth are the same to me—both have the flash of enlightenment, the almost incredibly enhanced vision, and the ecstacy and euphoria of released tension. At the same time, discovering a new truth, similar in subjective pleasure to understanding an old one, is in one way quite different. The difference is the pride, the feeling of victory, the almost malicious satisfaction that comes from being first. “First” implies that someone is second; to want to be first is asking to be “graded on the curve”. I seem to be saying, almost, that clarifying old mathematics is more moral than finding new, and that’s obviously silly—but let me say instead that insight is better without an accompanying gloat than with. Or am I just saying that I am better at polishing than at hunting and I like more what I can do better?
P. Halmos (1985), I want to be a mathematician, Springer
从我读过的所有Halmos著作来看,他不愧于自传的第一句话。我常常能折服于他行文的文笔。看他的书,经常只是廖廖数行简单的句子,某种思想就能钻进你的脑袋里。
因此我推荐,上述我所读过的他的书,为相关话题的书的首选、必读。
我读很多数学书都不做习题,或者有限地选做一些习题。但是Halmos的书不光是必须完成每道习题,而且他正文中的每句断言,凡是你不太清楚理由的,都值得简单证明一遍。所幸的是他的书都很薄。