[mathjax]
通过上一篇我们已经学会怎样通过Fourier变换重构应变和应力的波形。至少In/1是已经可以直接用Fourier变换的结果计算了。本文先介结实际实验数据的导入，再继续上一篇的话题介绍如何计算In/1和其余的LAOS参数。
LAOS实验是怎么实施的
我们是在TA ARES-RFS流变仪上做LAOS实验。公司的名字：TA Instruments。这是一台应变控制型流变仪（strain-controlled rheometer），相比之下同公司的AR-G2则是应力控制型（stress-controlled）。这个小册子上介绍了ARES和AR-G2两台流变仪的特点，其中的原理图和具体参数可以用在毕业论文中。进行LAOS实验需要流变仪持续对样品施加正弦应变，我们是利用流变仪控制软件TA Orchestrator 7.2.1自带的测试模式dynamic time sweep来控制流变仪进行这一操作。Dynamic time sweep是固定振荡的应变幅度γ0和频率ω，测量G’和G”随时间变化的测试，所以正适合我们。在Orchestrator软件中设定好dynamic time sweep的应变和频率，仪器就会以相应的正弦函数去控制马达了。此时，我们需要马上从仪器背后的模拟输出端口同时读出仪器的测量信号，并用一个数模转换器（analog-to-digital converter, ADC）转换成数字信号，输入到计算机。我们用的ADC是NI USB-9215A，要通过电脑来控制它何时开始和停止采样，以及以多大的采样频率进行采样。许多软件都可以通过它的驱动程序接口来实施控制（MATLAB本身就可以），在LAOS实验中我们用一个LabView开发的工具FT Meassurement来采集数据。因此，我们用一台电脑，用两个软件分而控制不同的过程。Orchestrator控制流变仪的运作，而FT Meassurement控制ADC。这一流程图可参考[1]和[2]中的用图。具体信号线接法和处理方式见下面的PPT（可下载）。
上篇文章也说过，从流变仪采集到的一个是马达位移的电压信号，另一个是力矩的电压信号，它们都要乘以一个系数，才是应变和应力。从ARES流变仪的说书中可以查到背板输出信号的具体情况：
- TORQUE OUT：从0到满量程，对应电压是0 ~ 5 V。由于转矩可以有两个方向，所以总的电压范围就是-5 ~ +5 V
- STRAIN OUT：虽然标记是STRAIN，但其实只是马达转动的角位移。从0 ~ 0.5 rad对应电压是0~5V，考虑两个转动方向，总电压范围是-5~+5 V
TORQUE OUT的“满量程”到底是多少呢？由于我们的ARES有两个档位的力矩传感器。Xducer 1的传感器叫做“20g FRT”。20g是指该档位的最大量程是20 g·cm，力矩的一个非SI单位，SI单位是N·m。1 g·cm = 98.066E-6 N·m。可以去此网站进行换算。FRT是force rebalance transducer的缩写，这是ARES的传感器采用的一种技术（参考）。所以20g FRT的最大量程是1.96E-3 N·m。另一个档位Xducer2是1k FRT，也就是最大量程是0.0981N·m。因此，到底TORQUE OUT输出的电压值对应多大的力矩，要看当时仪器在线的传感器档位是Xducer1还是Xducer2。以下是更详细的参数：
| Transducer | 1 | 2 |
| Transducer Description | 20g FRT | 1k FRT |
| Maximum Torque (g·cm) | 20 | 1000 |
| Minimum Torque (g·cm) | 0.004 | 1 |
| Torque Calibration Value | 21.34 | 1050.7 |
| Torque Compliance | 6.67E-06 | 6.67E-06 |
| Inertia Constant (g·cm^2) | 660 | 660 |
| Phase Adjust Constant (rad·s/rad) | -5.80E-05 | -5.80E-05 |
| Maximum Normal Force (g) | 2000 | 2000 |
| Minimum Normal Force (g) | 2.00E+00 | 2.00E+00 |
| Normal Calibration Value | 2101.8 | 2101.8 |
| Normal Compliance (um/kg) | 0.00E+00 | 0.00E+00 |
| Phase Offset (rad) | 0 | 0 |
| Motor Temp Reference (°C) | 3.27E+01 | |
| Motor Temp Gain | 2.9445 | |
| Compliance Gain | 7.89E-01 | |
记STRAIN OUT输出电压为Vs，TORQUE OUT输出电压为Vt，换算成相应的角位移θ转矩M的公式是：
、
，其中，转换系数kt = 0.1 rad/V，kt,1 = 3.92E-4 N·m/V，kt,2 = 0.0196 N·m/V。从角位移（rad）到应变（量纲一量），以及从转矩（N·m）到应力（Pa），还各需要乘一个系数Fγ和Fσ，这个系数跟所选用的夹具种类和尺寸有关。流变仪的说明书会介绍各种夹具的系数如何从夹具的尺寸来换算。这里只举锥板夹具的例子：
Figure 1 Cone-plate geometry
$$F_\gamma=\frac{1}{\tan\alpha},\quad F_\sigma=\frac{3}{2\pi R^3}$$所以，最终的应变和应力应该是$$\gamma=F_\gamma k_\text{s}V_\text{s},\quad\sigma=F_\sigma k_{\text{s},i}V_\text{t}$$
实验数据处理
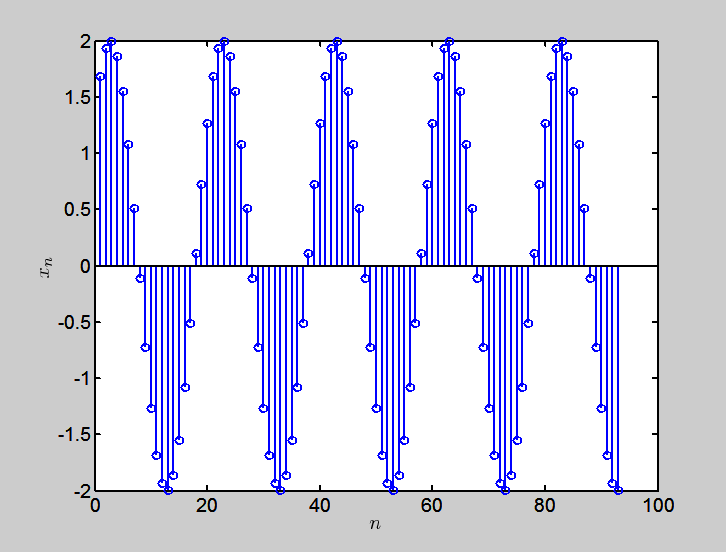
从仪器背板TORQUE OUT和STRAIN OUT连线到ADC的channel 1和channel 2输入，然后在计算机中的FT Measurement控制ADC以一定的采样频率fs进行采样，就会生成一个文本数据文件，此例的文件名是“DTimeSwp (13) 000 .txt”。第一行是一些说明性的数字，然后就是两列数据，分别对应着channel 1和channel 2的电压测量值，按照通常的接线方式，第一列是STRAIN OUT信号，第二列是TORQUE OUT。在MATALB中预览出下：
Figure 2 Data file from FT Measurement
用importdata命令可以自动处理具有表头的数据文件，把表头文字和数据分开。
clear all
clc
A=importdata('DTimeSwp (13) 000 .txt')
观察A的返回信息。如果源文件没有表头，是纯数据，A就是直接由这些数据组成的矩阵；如果有表头，A就是一个struct类型，包含一个data单元和一个textdata单元。textdata是以表头为内容的字符串，data单元就是数据组成的矩阵。要调用data，语法是A.data。为了简单，就把数据重新放在一个新的变量中：
x=A.data;
DTimeSwp (13) 000 .txt这个文件，对应的是一个dynamic time sweep测试，命令的应变幅度γ0 = 160%，角频率是ω = 6.283 rad/s（f = 1.0 Hz）。FT Measurement控制ADC以fs = 200 Hz的采样频率进行采样。我们可以从fs重构一列时间数据，拼到变量x中：
fs=200; % the sampling frequency was fixed by the test condition
t=0:1/fs:(length(x)-1)/fs; % construct the time series
t=t(:);
x=[t x]; % combine the time series and the signals
这样，变量x第一列是时间，第2、3列才分别是STRAIN OUT和TORQUE OUT电压信号。这个实验是用一个锥板夹具来做的，直径50 mm，锥度0.04 rad。测试时，在线传感器是xducer 1。因此根据计算公式，Fγ = 24.99，Fσ = 30557.75，ks和kt,1的值前文已经过了。把x变量的数据转换成应力和应变：
% set all the coefficients
F_gamma=24.99;
F_sigma=30557.75;
ks=0.1;
kt1=3.92e-4;
% convert voltage to strain/stress
x(:,2)=F_gammaks.x(:,2);
x(:,3)=F_sigmakt1.x(:,3);
获取信号的频率
至此，对变量x的波形重构可以完全跟之前文章介绍的一样的，不再重复。但是本文再作一项改进。前面几篇文章说过，实际应变值跟软件设定的命令有可能有所偏差，加上仪器噪音的影响，所以我们要重构应变的信号来准确获得实际的应变幅度和频率。而准确的FFT结果要求待做FFT的信号是“相干取样”的。做相干取样又要求我们至少要准确知道信号的频率。解决这一矛盾的方法是，利用应变必然是正弦波的性质，先通过正弦函数拟合来获取信号的应变和频率。事实上，对于一个正弦波，正弦拟合和FFT都是重构的方法，但实际上正弦拟合的幅度和相位往往不准，所以只要能做好相干取样，我们都偏爱用FFT做重构；但是正弦拟合得到的频率是准的，而这时我们只需要知道一个频率，因此可以采用正弦拟合来完成。
我们调用一个别人开发的代码进行：sinfapm。其语法在代码开头的注释文件中有清楚的介绍。注意，sinfapm代码又调用了另一个用于进行非线性最小平方求解的第三方代码：LMFnlsq，需要都放在同一个文件夹。
sinfapm函数还有一个麻烦之处，就是处理取样频率太高的数据会失效。所以，在使用前要临时对一个未知信号“降采样”（down sampling）。经验表明，对每个周期不超过1000个数据点的数据，sinfapm能够稳定表现。因此就是在使用sinfapm前要加一段代码，如果信号每周期超过1000个点，就降采样为每周期1000个点；否则就不变。麻烦的是，为了知道原信号每周期有多少个点，我们还是要先知道信号的频率。所幸，这一步只需要粗略估算即可，因此，做一个不靠谱（没有相干采样）的FFT粗估一下频率就行了。总之，整个精确获得频率的步骤就是：
- 用FFT粗估频率
- 根据粗估频率计算信号每周期有多少个数据点，决定降取样比值
- 对降取样的数据进行正弦拟合得到精确的频率
以下是代码：
% Roughly estimate the input frequency by FFT
N=length(x);
Xraw=fft(x(:,2)); % needless to renormalized the amplitude coz we only want the frequency
% find the maximum peak and obtain the corresponding row index
% the first data is the DC component which is omitted because the value may
% be higher than the first harmonic and violate the peak finding
[I, J]=max(abs(Xraw(2:end)));
% I is useless
% estimate the points per cycle of the signal
pts_per_cycle=N/J;
if pts_per_cycle > 1000
% select 1 out of every jump data to reach 1000 points per cycle
jump = floor(pts_per_cycle/1000);
else
jump=1;
end
[f, amp, phi]=sinfapm(x(1:jump:end,2),fs/jump);
% amp and phi are useless
f
我们可以作图验证sinfapm是否正常工作了：
plot(t,ampsin(2pift+phi),'r-',t,x(:,2),'bo') % Figure 3
Figure 3 Effect of sinfapm
连幅度和相位都拟合得这么好，频率的拟合结果应该是可信的了。频率知道了之后，剩下的事情就不新鲜了，参见前一篇文章。
N=length(x);
pts_per_cycle=fs/f;
N_cycle=floor(N/pts_per_cycle);
N_cut=round(round(N_cycle/3)*pts_per_cycle); % use the last third of cycles
x=x(length(x)-N_cut:end,:); % crop the last N_cut data
Xraw=2*fft(x(:,2))/N_cut;
Xraw=Xraw(1:ceil(N_cut/2));
freq=0:fs/N_cut:fs/2-fs/N_cut;
A=abs(Xraw(round(N_cutf/fs)+1));
delta0=wrapTo2Pi(angle(Xraw(round(N_cutf/fs)+1))+0.5pi);
frq=freq(round(N_cutf/fs)+1); % this line can be omitted and use the f instead
x_rec=A.sin(2pifrq.x(:,1)+delta0); % frp can be replaced by f
Yraw=2*fft(x(:,3))/N_cut;
Yraw=Yraw(1:ceil(N_cut/2));
max_nr_harm=floor(fs/(2*f));
if max_nr_harm/2==floor(max_nr_harm/2)
max_nr_harm=max_nr_harm-1;
end
max_nr_harm=max_nr_harm-2;
if max_nr_harm>25
max_nr_harm=25;
end
I_n=zeros((max_nr_harm+1)/2,1);
delta_n=zeros((max_nr_harm+1)/2,1);
for i=1:(max_nr_harm+1)/2
I_n(i)=abs(Yraw(round((2i-1)N_cutf/fs)+1));
delta_n(i)=angle(Yraw(round((2i-1)N_cutf/fs)+1))+0.5pi;
end
DC=abs(Yraw(1))cos(angle(Yraw(1)))/2;
y_rec=zeros(length(x(:,3)),1); % create the variables for the reconstructed signals
for i=1:2:max_nr_harm
y_rec=y_rec+I_n((i+1)/2).sin(i2pif.*x(:,1)+delta_n((i+1)/2));
end
y_rec=y_rec+DC;
plot(x(:,2),x(:,3),'b-',x_rec,y_rec,'r-') % Figure 4
看效果：
Figure 4 Reconstruction of the LAOS results.
我们的信号是已经转换成应力和应变的了。因此，Figure 4中横轴是应变，正负最值都是1.6，与软件命令值（160%）相符。我们换一个应变幅度为250%实验数据，结果如下：
Figure 5 Reconstruction of LAOS data
γ0 = 250%时已有明显的非线性粘弹性。
计算非线性粘弹性参数
我们平时所说的G’和G”，是FFT之后的基频幅值计算的。在线性粘弹性条件下，FFT之后只有一个基频帐，G’和G”是“储能模量”和“损耗模量”。但是在非线性粘弹性条件下，G’和G”只是许多n倍频谐波中的基频分量（n = 1），它们也没有“储能”或“损耗”的概念了。这一点要先搞清楚。
计算G’和G”：
delta=wrapTo2Pi(delta_n(1)-delta0);
G_p=cos(delta)I_n(1)/A;
G_pp=sin(delta)I_n(1)/A;
In/1也可以直接计算：
In1=I_n(2:5)/I_n(1);
如何求切线
现在我们来计算GM、GM和Gk参数。它们的定义已在上一篇文章中给出。根据定义，需要对曲线进行求导。在MATLAB如何做呢？按定义一步步来。
一个已经离散化了的曲线，要在曲线上某几何位置求切线，很可能并没有数据恰好落在这个点上，只能使用这个几何位置邻近的两个数据点，以这两个点所确定的直线作为切线。所以，如果一条曲率较大的曲线，离散化的取样频率又很低，那么很可能两个数据之间相隔很远，按以上办法求出来的切线与理想情况就会相差很远。也就是说，对离散数据求导的效果非常依赖于信号的取样质量（就是取样频率够不够高）。
其次，如果信号有噪音，那么作出的切线斜率将非常容易受噪音影响。在数值方法中，求导是一个放大噪音的操作。一个信号，很可能不求导的话，噪音还在可以接受的范围；一旦求导之后噪音就使信号无法分辨。因此，对离散数据求导的效果又非常依赖于信号的信噪比。
因此为了求得准确、稳定的导数，我们要采取一系列的办法。第一当然就是测试的时候让ADC以最高的采样频率进行采样（100 kHz）。
第二，这样高的采样频率，完全可以进行降采样（down sampling）。但我们的降采样方法不是像前文用过的那样简单地扔掉部分数据点——这样对于去噪没有任何效果——而是每几个数据点做一次平均值，这样的做法叫decimation，它的效果相当于使样品经过一个低通滤波品，把高于一定频率的信号消除掉。如果我们每N个数据取一个平均值，那么decimation之后的取样频率就是100000/N Hz。一开始，用远高于需要的取样频率取，称作过取样（oversampling）。Oversampling和decimation是信号采集中的一个基本操作，作为一种提供信噪比的标准步骤。使用FT Measurement采集的流变数据的时候，该软件是同时做了oversampling和decimation的，最终得到的文本数据文件的采样频率是decimation之后的采样频率。这方面内容，也可以参考我的博士论文的第二章。
第三，我们按照LAOS的假设（应力波型只有奇次谐波）对信号进行重构，用一个光滑的、公式计算的曲线来代替实验测得的、带有噪音的曲线。重构曲线是完全没有噪音的。这还不够——
第四，由于信号有很多个周期，那些过零点、最值点之类的几何位置，信号不止经过一次。那么，我们就把每次经过的这些位置所能作出的切线斜率都算出来，然后对这么多个周期得到的斜率曲一个平均值，进一步消除不同周期处的细微差别。
只有做足以上四个方面，才能比较保证地对绝大多数实测的LAOS数据进行准确可靠的求导操作。
在MATLAB中如何在重构的Lissajous曲线上找到要作切线的几何位点？根据定义，GM要找γ = 0，GL要找γ = γ0，Gk要找σ = 0。我们需要确定这些几何位置邻近的两个数据点处在数据列中的第几行。以GM的计算为例（找γ = 0）。这相当于要找数据x_rec中取值经过零位的行。而且，我们只关心从小于零变成大于零的地方（这里默默假设了x_rec是没有直流分量的，如果有直流分量，x_rec波形的零位就不落在取值为零处，除非另把DC分量减去）。首先，我们把x_rec数据所有大于零的值标为1，小于零的值标为0。
A=x_rec;
A(A>0)=1;
A(A<0)=0;
在A这个临时变量，凡是导数不为零的地方就是转折点（不是从1变到0就是从0变到1），这些不为零的导数，不是等于1就是等于-1。由于我们只关心x_rec中从小于0变成大于零的地方，所以我们相当于只关心A的导数等于1的地方。
zero_ind=find(diff(A)>0);
以上用到的一些用逻辑式调用矩阵单元的方法，和find命令等，可以自己复习MATLAB的help。zero_ind就是x_rec中取值从负到正的第一个数据，即它是负的，然后第zero_ind+1是正的。我们可以临时作个图看看，我们找到的zero_ind位置都对不对：
plot(1:length(x_rec),x_rec,'-',zero_ind,zeros(length(zero_ind),1),'o') % Figure 6
Figure 6 Effect of zero finding
求导、取平均，得到GM：
G_M_raw=(y_rec(zero_ind+1)-y_rec(zero_ind))./(A(zero_ind+1)-A(zero_ind));
G_M=mean(G_M_raw);
我们可以再临时作个图看看这个切线取准了没有。但为作这个图，要先确定真实的位点在哪儿（不能还用那两个邻近数据点）。这个点，应该是两个相邻点所确定的直线与x = 0直线的交点。同样，这个交点也可以通过多个周期求平均而更为准确地确定。最终要作的切线，就是一条过这一交点，斜率为GM的直线，利用简单解析几何知识即可作出：
y_m_raw=-G_M_raw.x_rec(zero_ind+1)+y_rec(zero_ind+1);
y_m=mean(y_m_raw);
lx=min(x_rec):0.01:max(x_rec);
ly=G_M.lx+y_m;
plot(x_rec,y_rec,'-b',lx,ly,'-r') % Figure 7
Figure 7 Effect of G_M calculation
GL要找γ = γ0，即找x_rec中的最值。先对x_rec进行求导，问题就还原成找x_rec求导后的过零位，除了多一步求导之外，其余跟刚才的代码完全相同。注意的时，y_rec有明显的直流分量，计算时要减去。
A=diff(x_rec);
A(A>0)=1;
A(A<0)=0;
zero_ind=find(diff(A)<0);
G_L_raw=(y_rec(zero_ind)-DC)./x_rec(zero_ind);
G_L=mean(G_L_raw);
Gk是找σ = 0：
A=y_rec-DC;
A(A>0)=1;
A(A<0)=0;
zero_ind=find(diff(A)>0);
A=y_rec-DC;
G_k_raw=(A(zero_ind+1)-A(zero_ind))./(x_rec(zero_ind+1)-x_rec(zero_ind));
G_k=mean(G_k_raw);
至此，我已经完整地介绍了如何从实验获得的LAOS数据求出相应的非线性粘弹性参数。我再总结一下流程：
- 做实验，设定ADC采集参数进行数据采集（同时已进行oversampling和decimation，规定了信号的fs）
- 通过对应变信号进行粗估和正弦拟合，获得实验的准确测试频率
- 对应变和应力信号进行重构
- 按照定义求得各非线性粘弹性参数
如果对实验体系以一系列的应变幅度进行了LAOS实验，然后想考察非线性参数随应变幅度的变化；那么，可以对每个应变幅度得到的LAOS数据做以上同样的操作，既编写一个循环结构来完成。这样的办法将在后面的文章中看到例子，此处不单独举例了。后面的文章主要介绍如何用流变学模型的结果（例如Giesekus模型)来拟合实验数据。
References
- K. Hyun, M. Wilhelm, C.O. Klein, K.S. Cho, J.G. Nam, K.H. Ahn, S.J. Lee, R.H. Ewoldt, and G.H. McKinley, "A review of nonlinear oscillatory shear tests: Analysis and application of large amplitude oscillatory shear (LAOS)", Progress in Polymer Science, vol. 36, pp. 1697-1753, 2011. http://dx.doi.org/10.1016/j.progpolymsci.2011.02.002
，测量应力的响应
，即
，以及
，来表征非线性粘弹性的程度（即
和频率
，但是，由于仪器误差，实际施加在样品上的应变幅度和频率，未必完全等于的命令值。尽管这一误差非常小，但从做法上我们还是要以实际应变信号为准。所以，我们首先要对实际应变信号进行判断，获得实际的应变幅度和频率。如何判断一个未知正弦信号的振幅、频率和相位的方法已经在上一篇文章中介绍了。
和
同样需要对
，但是实际上我们根据需要取有限的n个高次谐波，就可以比较准确地重构出
、
和
.
![x\left(t\right)=A\sin(\left[2\pi f\left(t-1.6\right)\right]=A\sin(\left(2\pi ft+\delta\right)](https://mlnbqvqmzkw4.i.optimole.com/w:293/h:16/q:mauto/f:best/https://www.andrewsun.net/panta_rhei/wp-content/ql-cache/quicklatex.com-a6de99eb1c915d085bd379f899fef14a_l3.png "Rendered by QuickLaTeX.com")
，则相位角
，换成0到2π之间就是
。若取时移是1.7 s得
，所以δ应该在0.9425到1.2566之间。从图中还能读出振幅A = 2，则信号
。用正弦函数去拟合Fig. 2的序列发现其实最精确的函数描述应该是
，见Fig. 3。
