[mathjax]
上一篇介绍了用Fourier变换来重构一个未知正弦信号的方法。本篇介绍对于未知非正弦信号的情况。
大幅振荡剪切的参数
大幅振荡剪切实验产生的波形是非正弦信号,非正弦是非线性粘弹性的特点。所以对非线性粘弹性程度的表征,就是对波形正弦形状偏离程度的表征。关于大幅振荡剪切和非线性粘弹性的原理与实践,可见Hyhn等的综述[1],或者参阅我的博士学位论文第1.2.1节、第1.3节和第2章。本文只解决MATLAB编程实现问题。
大幅振荡剪切(LAOS)实验中,我们从流变仪同时获取两个信号。一个是应变的信号,一个是应力的信号(事实上,一个是马达位移信号,另一个是力矩信号,它们都要乘以一个系数,才是应变和应力。此文先略去这一事实了)。在应变控制的实验中,我们施加一个正弦的应变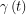 ,测量应力的响应
,测量应力的响应 ,即
,即
$$\begin{cases}\gamma\left(t\right)=\sin\omega t\\ \sigma\left(t\right)=\sum_{n=0:\text{odd}}^\infty\sigma_n\sin\left(\omega t+\delta_n\right)\end{cases}$$由此式可定义LAOS实验结果的表征参数 ,以及
,以及 ,来表征非线性粘弹性的程度(即
,来表征非线性粘弹性的程度(即 偏离正弦函数的程度。此外,我们还会以
偏离正弦函数的程度。此外,我们还会以 对
对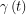 作图(参数方程作图),得到Lissajous曲线。然后用曲线的形状特征来表征非线性粘弹性的程度(即曲线偏离椭圆的程度)。描述曲线形状特征,往往就是各种各样的切线斜率(可自行上网搜索复习参数方程求导)。在LAOS中常用:$$G_\text{M}=\left.\frac{d\sigma}{d\gamma}\right|_{\gamma=0}$$$$G_\text{L}=\frac{\sigma{\gamma_0}}{\gamma_0}$$$$G_\text{k}=\left.\frac{d\sigma}{d\gamma}\right|_{\sigma=0}$$
作图(参数方程作图),得到Lissajous曲线。然后用曲线的形状特征来表征非线性粘弹性的程度(即曲线偏离椭圆的程度)。描述曲线形状特征,往往就是各种各样的切线斜率(可自行上网搜索复习参数方程求导)。在LAOS中常用:$$G_\text{M}=\left.\frac{d\sigma}{d\gamma}\right|_{\gamma=0}$$$$G_\text{L}=\frac{\sigma{\gamma_0}}{\gamma_0}$$$$G_\text{k}=\left.\frac{d\sigma}{d\gamma}\right|_{\sigma=0}$$
MATLAB编程步骤
在详细介绍MATLAB代码之前,先总结一下我们要完成什么任务,跟从哪些步骤。我们的任务就是要从应力和应变的信号计算出上述的这么多参数。实验时,我们会规定应变的幅度 和频率
和频率 ,但是,由于仪器误差,实际施加在样品上的应变幅度和频率,未必完全等于的命令值。尽管这一误差非常小,但从做法上我们还是要以实际应变信号为准。所以,我们首先要对实际应变信号进行判断,获得实际的应变幅度和频率。如何判断一个未知正弦信号的振幅、频率和相位的方法已经在上一篇文章中介绍了。
,但是,由于仪器误差,实际施加在样品上的应变幅度和频率,未必完全等于的命令值。尽管这一误差非常小,但从做法上我们还是要以实际应变信号为准。所以,我们首先要对实际应变信号进行判断,获得实际的应变幅度和频率。如何判断一个未知正弦信号的振幅、频率和相位的方法已经在上一篇文章中介绍了。
然后,就要处理应力的信号。为了获得 和
和 同样需要对
同样需要对 进行fft处理,方法跟上一篇文章介绍的类似,区别只在于我们除了要获得基频的幅值和相位之外,还要获得高次谐波的幅值和相位。理论上来说
进行fft处理,方法跟上一篇文章介绍的类似,区别只在于我们除了要获得基频的幅值和相位之外,还要获得高次谐波的幅值和相位。理论上来说 ,但是实际上我们根据需要取有限的n个高次谐波,就可以比较准确地重构出
,但是实际上我们根据需要取有限的n个高次谐波,就可以比较准确地重构出 的波形了。提醒一下,定义式里应变是一个零相位的标准正弦函数,但实际重构的应变波形可能会有非零的相位,这时,应力的各个谐波的相位要都减去应变的相位,才是我们要求的
的波形了。提醒一下,定义式里应变是一个零相位的标准正弦函数,但实际重构的应变波形可能会有非零的相位,这时,应力的各个谐波的相位要都减去应变的相位,才是我们要求的 。
。
Lissajous曲线的各种导数,要同时在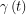 和
和 都重构了之后,再进行求导计算得到。总而言之,要完成以下三个步骤:
都重构了之后,再进行求导计算得到。总而言之,要完成以下三个步骤:
- 重构应变
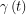 ,获得
,获得 、
、 和相位
和相位
- 重构
 ,获得
,获得 和
和 ,计算
,计算
- 用重构的
 和
和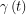 作Lissajous曲线,以及计算
作Lissajous曲线,以及计算 、
、 和
和
重构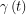 和
和
MATLAB帮助文件里fft命令的条目有一个范例,应该能解决大部分问题了。其中在coherent sampling(见上篇文章)处,范例用next power of 2,其实没有必要。下面的代码,我就不多作解释了。
clear all
clc
% the strain signal
fs=1000; % sampling frequency
t=0:1/fs:30.2; % the time series of the strain signal
t=t(:); % convert to colume vector
w=5; % (rad/s) the angular frequency of the strain signal
f=w/(2*pi); % (Hz)
x=250sin(2pift+1)+25randn(size(t)); % strain signal with noise
y=1.001+8.1532.sin(2pif.t+2.5936)+2.4952.sin(6pif.t+0.5199)+...
0.8856.sin(10pif.t+4.3353)+0.2932.sin(14pif.t+1.8641)+...
0.0992.sin(18pif.t-0.6417)+0.0282sin(22pif.+3.3818)+...
0.2randn(size(t)); % stress signal with noise
[AX,H1,H2]=plotyy(t,x,t,y,'plot'); % Figure 1
set(AX(1),'XLim',[0 8])
set(AX(2),'XLim',[0 8]) % set the time axes

Figure 1 Parts of the strain and the stress signals
两个信号都加入了噪音,而且应力信号加入了直流分量,更接近真实的情况。另一个真实的情况是,应力响应的波形往往需要经过几个周期之后才达到稳定的形状。我们当然是取稳定之后的波形来进行Fourier变换,因此就要截取后几个周期。
N=length(x);
N_per_cycle = fs/f; % average points per cycle
N_cycles = floor(N / N_per_cycle); % maximum number of complete cycles
N_cut=round(15*N_per_cycle); % use the last 15 cycles
t=t(length(t)-N_cut:end);
x=x(length(x)-N_cut:end);
y=y(length(y)-N_cut:end);
% crop the last N_cut data.
接下来,先对应变信号进行重构,方法跟上篇文章一样。
Xraw=2fft(x)/N_cut;
Xraw=Xraw(1:ceil(N_cut/2));
freq=0:fs/N_cut:fs/2-fs/N_cut;
A = abs(Xraw(round(N_cutf/fs)+1))
delta = wrapTo2Pi(angle(Xraw(round(N_cutf/fs)+1))+0.5pi)
frq = freq(round(N_cutf/fs)+1)
x_rec=A.sin(2pifrq.*t+delta);
plot(t,x,'b-',t,x_rec,'-r')

Figure 2 Reconstruct the strain signal
然后轮到应力的波形。先看看它的Fourier变换结果:
Yraw=2*fft(y)/N_cut;
Yraw=Yraw(1:ceil(N_cut/2));
plot(freq, abs(Yraw)) % Figure 3

Figure 3 Amplitude spectrum of the stress signal
放大最左边的部分,可以看到好多高次谐波。为什么右边有这么长的多余部分?回忆上篇文章。Fourier变换后的频率范围等于fs/2。我们fs达到1000 Hz,而信号主频只有约0.8 Hz,几个高次谐波都集中在最左侧了。有时间的话,最好多点尝试不同信号的FFT,熟悉这一转换是认识大自然的一个新的思想高度。因为大自然很多自然过程就是在做Fourier变换。例如X线穿过晶体发生衍射,光就被Fourier变换了,形成的二维斑点图可通过进行二维的反Fourier变换,还原成样品中的晶格排布。所以我们总是说,X射线的图谱是“倒易空间”(Fourire变换前后坐标变倒数了)。
Figure 3还可看到,在频率为0处有一个峰。这个峰是原波形的直流分量(见文章开头构建信号的式子),我们需要知道各个谐波在信号序列中的具体位置。上篇文章已经解决了正弦信号的情况,对于高次谐波(都是奇数倍频),只要相应地乘以3、5、7即可。但是,根据定义式,应力的Fourier展开理论上是无穷多项的,而实际上也需要取尽量多项以确保最准确地重构原波形。到底Fourier变换之后,最多允许看到多少个高次谐波呢?这就相当于要找使nf<fs/2的最大奇数n。不过,如果信号的取样频率fs相当大,最大谐波次数n也会非常大,我们实在没必要取这么大的n(如Figure 3的情况右边大部分是多余的。因此我们又人为规定最大谐波次数不超过25个,就是说我们假定25个高次项对于再怎么非线性的信号都肯定足够了。以下是相关的代码:
max_nr_harm=floor(fs/(2*f)); % Maximum number of harmonics
if max_nr_harm/2==floor(max_nr_harm/2)
max_nr_harm=max_nr_harm-1;
end
% maxmum odd number of harmonic
max_nr_harm=max_nr_harm-2; % fall back one more odd harmonic for safety
if max_nr_harm>25
max_nr_harm=25;
end
接下来就是要确定这些谐波的幅值和辐角:
% create the variables for harmonic amplitudes and phase angles
I_n=zeros((max_nr_harm+1)/2,1);
delta_n=zeros((max_nr_harm+1)/2,1);
for i=1:(max_nr_harm+1)/2
I_n(i)=abs(Yraw(round((2i-1)N_cutf/fs)+1));
delta_n(i)=angle(Yraw(round((2i-1)N_cutf/fs)+1))+0.5pi;
end
DC=abs(Yraw(1))cos(angle(Yraw(1)))/2;
其中,直流分量的大小计算方法为什么是这个,我不太记得了。这时,你已经可以通过I_n(i)和delta_n(i)来计算相应的非线性粘弹性参数 和
和 了。再次提醒,应力波形的各谐流相位角要减去应变波形的相位角,才是定义式中的相位角。我们也可以检验一下重构的应力波形:
了。再次提醒,应力波形的各谐流相位角要减去应变波形的相位角,才是定义式中的相位角。我们也可以检验一下重构的应力波形:
y_rec=zeros(length(y),1); % create the variables for the reconstructed signals
for i=1:2:max_nr_harm
y_rec=y_rec+I_n((i+1)/2).sin(i2pif.*t+delta_n((i+1)/2));
end
y_rec=y_rec+DC;
plot(t,y,'-b',t,y_rec,'-r') % Figure 4

Figure 4 Reconstructed stress signal
作成Lissajous曲线来看:
plot(x,y,'b-',x_rec,y_rec,'r-')

Figure 5 Reconstructed Lissajous curve
可见,通过Fourier变换重构波形,可以很好地把噪音排除掉。Lissajous曲线的各个形状参数,需要在曲线上找各种交点求切线(见定义式)。如果在原信号的基础上直接做,可想而知误差会有多大。这就是为什么我们明明已经有信号不直接用要先重构一番的原因。具体如何在Lissajous曲线上找点、求切线的方法,在下一篇文章中介绍。
References
-
K. Hyun, M. Wilhelm, C.O. Klein, K.S. Cho, J.G. Nam, K.H. Ahn, S.J. Lee, R.H. Ewoldt, and G.H. McKinley, "A review of nonlinear oscillatory shear tests: Analysis and application of large amplitude oscillatory shear (LAOS)", Progress in Polymer Science, vol. 36, pp. 1697-1753, 2011. http://dx.doi.org/10.1016/j.progpolymsci.2011.02.002






