[mathjax]
为了带师弟做实验，简要总结一下在MATLAB里进行Fourier变换的一些代码，以供大家参考。
Discrete Fourier transform (DFT): The sequence of N complex numbers x0, …, xN-1 is transformed into an N-periodic sequence of complex numbers according to the DFT formula
.
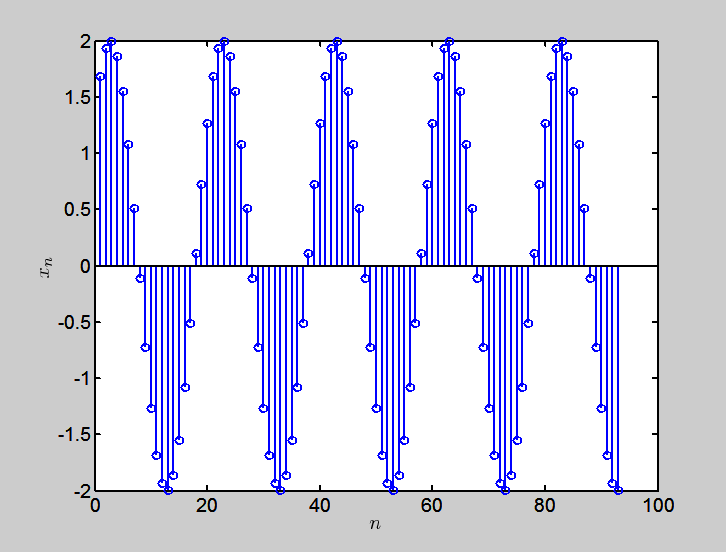
一般把变换前的信号xn当成时域信号，变换后的Xk当成频域信号。可见，时域是N个单元的信号，变换后频域还是N个单元的信号。什么周期啊频率啊这些信息是暂时没有的。例如xn为以下这个序列（Fig. 1），横坐标就是序号n。这段序列，可以是一段10秒钟的的信号，也可以是一段100秒钟的信号。当然，实际情况下一段信号是多少秒是事先知道的，出来的信号一共有多少个单元值（N）则取决于我们隔多长时间取一次样。如果一段10秒钟的信号，我们每秒取一次样，这个序列就有10个单元（N = 10）。反之，Fig. 1的这个序列N = 93，假如这个信号是每隔0.1秒取一次样得到的，这个信号的总时长就是9.2秒；而假如这个信号是每隔10秒取一次样得到的，这个信号总时长就是920秒了。每隔多长时间取一次样，可以用取样频率fs来表示。fs = 10 Hz就是每隔0.1 s取一次样。所以，为了给一对离散Fourier变换xn和Xk赋以周期或频率的信息，必须给时域信号规定一个fs。一旦fs规定了，周期和频率也就规定了。还拿Fig. 1的序列为例，设该序列的取样频率fs = 10 Hz，则该序列每个单元隔了0.1 s。我们可以数一下这个序列一个周期有多少个单元——20个，那么该序列的周期T = 2 s，频率f = 0.5 Hz。
Figure 1
事实上Fig. 1的序列是一个有一定时延的正弦序列（即不是从零开始），我们已经根据规定的fs知道了它的周期和频率，不仿就把它改作在时间轴上（Fig. 2）。
Figure 2
可以看到，该正弦信号的零位在第17和第18个单元之间，即在1.6 s到1.7 s处，以1.6 s计算，该信号可写成![x\left(t\right)=A\sin(\left[2\pi f\left(t-1.6\right)\right]=A\sin(\left(2\pi ft+\delta\right)](https://mlnbqvqmzkw4.i.optimole.com/w:293/h:15/q:mauto/f:best/https://www.andrewsun.net/panta_rhei/wp-content/ql-cache/quicklatex.com-5d8960fccf9a2fdf12300d490089e90a_l3.png "Rendered by QuickLaTeX.com")
，则相位角
，换成0到2π之间就是
。若取时移是1.7 s得
，所以δ应该在0.9425到1.2566之间。从图中还能读出振幅A = 2，则信号
。用正弦函数去拟合Fig. 2的序列发现其实最精确的函数描述应该是
，见Fig. 3。
Figure 3
现在我们试着在MATLAB通过Fourier变换来精确地得到xn的幅值和相位，重构一个xn所对应的连续信号。首先构造上述的时域信号：
t = 0:0.1:9.2; % fs = 10 Hz
t = t(:); % convert into column vector
f = 0.5; % f = 0.5 Hz
x = 2 * sin(2 * pi * fi * t + 1)
前面说过对一组N个单元的序列进行Fourier变换之后得到的Xk也是一个N个复数单元的序列。我们看看它长什么样（分开模序列和辐角序列）：
Xraw = fft(x);
stem(abs(Xraw),'o'); % Figure 4
stem(angle(Xraw),'o'); % Figure 5
Figure 4
Figure 5
我们从Fig. 4可以看到结果跟我们想像的差很远。主要有以下四个问题：
- 频域谱分成了对称的两半。要取左边一半。但总单元个数为奇数（N = 93），到底是取46个还是47个？
- 若只看一半，频谱出现了单峰是没错（因为我们的信号只有一个频率），但它不是只在一个频率上，而是有一个很宽的分布，似乎我的输入信号的频率是“不纯”的——这并不符合事实
- 幅值不对，信号幅值是2，但频谱的峰高快到80了
- 横轴如何对应到真实的频率轴？
我们一个一个问题地解决。第一个问题，按照fft算法的规律，若N为偶数，则左右分成各N/2的两半即可；若N为奇数，则处于中央的那个单元是左右两半谱共用的。所以，无论取左半还是右半，都取(N+1)/2+1个。综合奇数和偶数的情况，对任意正整数N的取法就是对N/2向上取整。
N = length(x);
Xraw = Xraw(1:ceil(N/2));
stem(abs(Xraw));
第二个问题，之所以频谱的峰有一个很宽的分布，是由于谱泄漏（spectral leakage）现象，简单地说就是我们用来做Fourier变换的信号序列长度并不是恰好整数个周期。只有截取整数个周期来做Fourier变换，才能避免谱泄漏。可是对于一个未知频率的信号，我们本来就是要通过Fourier变换来知道它的频率，又怎么能在此之前就得知信号的周期呢？这种情况下，只能采用另一种方法，那就是把信号的首尾进行某种衰减处理，而这一处理在数学上又要保证不严重影响Fourier变换的结果，称为加窗操作（windowing）。详细的原理不在此详述。作为示范，我们可以利用我们对时域信号的已知信息来解决。已知信号周期T = 2 s，取样频率fs = 10 Hz，到底截取多少个点算一个周期呢？前面计算过了，20个点。干脆我们就只取一个周期得了，试试看：
x_cut = x(1:20); % N = 20
Xraw = fft(x_cut);
Xraw = Xraw(1:10); % N=20, so ceil(N/2) = 10
stem(abs(Xraw)); % Figure 6
Figure 6
这次，频峰值终于只出现在一个频率上了。而由于用来做Fourier变换的信号N减小到了20个，所以频域信号也就只有20个单元，取左半边就是十个单元。但我们看到，峰值也变了，原来近80，现在是在20。这说明，这个不正确的峰值，是跟N值有关的。这就涉及到第三个问题：峰值怎么校正回来。其实，我们做离散Fourier变换，需要进行归一化。但是怎么归一化，要看离散Fourier变换和反Fourier变换的具体规定，不同的书规定不一样。MATLAB里fft命令是需要用N来归一化的。但如果出来双面的频谱，各边就要用N/2来归一化。所以进行了归一化的的Fourier变换操作应为：
Xraw = 2 * fft(x_cut) / 20;
Xraw = Xraw(1:10);
stem(abs(Xraw));
出来的结果，峰值就会准确落在2（图略）。现在剩下最后一个问题，那就是横轴怎样换成真正的频率？这就要先了解Shannon-Nyquist定理。在此我只把结论说出来：频域信号单元的间格频率是fs/N。因此整个左半边谱的频率范围就是0 Hz ~ fs/2 – fs/N。为了解决奇数偶数问题（即以防fs/2不一定是fs/N的整数倍），最终我们就如下构造相应的频率轴：
freq = 0:fs/20:(ceil(N/2)-1)*fs/N;
freq = freq(:);
stem(freq,abs(Xraw)); % Figure 7
Figure 7
其实，要取整数个周期，不一定要只取一个周期。原时域信号至少有4个周期（见Fig. 1），所以我们可以取满整4个周期来做Fourier变换：
x_cut = x(1:80); % 4 cycles = 80 points
Xraw = 2 * fft(x_cut) / 80; % N = 80
Xraw = Xraw (1:40);
freq = 0:fs/80:fs/2-1/80;
stem(freq,abs(Xraw)); % Figure 8
Figure 8
可见，当我们多取几个周期时，Fourier变换的结果频率“分辨率”更高。因此为了获得尽可能完整地信息，要在保持取整个周期的同时，尽量取最多个周期来进行Fourier变换。我们把相应的辐角谱也作出来：
stem(freq,angle(Xraw); % Figure 9
Figure 9
我们发现，跟Fig. 5相比，Fig. 9的辐角谱显得非常杂乱无章。这是由于我们很好的消除了谱泄漏。规律：谱泄漏越严重，辐角谱越有序；谱泄漏避免得越彻底，辐角谱就越杂乱无章。虽然杂乱无章，但是模谱的幅值所在相应频率对应的辐角是应该是正确的。我们看看0.5 Hz处的辐角：
wrapTo2Pi(angle(Xraw(5))) % wrap result within 0 to 2Pi
结果不对，这是由于在MATLAB的fft得到的辐角差了π/2，要加上：
wrapTo2Pi(angle(Xraw(5))+0.5*pi)
这次就对了。
问题是，在实际应用中，我们不可能做一个Fourier变换，就作一次图，用肉眼看出峰值落在哪个频率上。必须事先就知道信号频率f在频域信号中的对应序号，直接就给出模的峰值和相应的辐角。所以，现在的问题是，如何不通过作图就知道，对于一个频率为f，采样频率为fs，N个单元的信号xn，进行了上述的Fourier变换后得到的Xk，第几个单元呢对应着f？这很简单，Fourier变换后的频率间隔是fs/N，因此，第Nf/fs+1个单元就是模的峰值所在频率。本例子中既可验证。
但是，假如信号的频率f在Fourier变换之后的频率轴上的位置，是恰好在频域信号两个单元之间呢？例如，我的信号频率是f=0.51 Hz，fs和N值不变，按照上述算法，要取第5.08个单元，当然不存在这个非整数单元。这就是说，我们要对Nf/fs+1这个公式加一个四舍五入的取整。注意，由于信号频率不同了，“整数个周期”的截取可能会略有不同。以下是具体的运算过程：
f = 0.51
x = 2 * sin(2 * pi * f * t + 1);
N = length(x);
N_per_cycle = fs/f; % average points per cycle
N_cycles = floor(N / N_per_cycle); % maximum number of complete cycles
N_cut = round(N_cycles * N_per_cycle); % number of points for FFT
x_cut = x(1:N_cut);
Xraw = 2 * fft(x_cut) / N_cut;
Xraw = Xraw(1:ceil(N_cut/2));
freq = 0:fs/N_cut:fs/2-fs/N_cut;
abs(Xraw(round(N_cut*f/fs)+1))
wrapTo2Pi(angle(Xraw(round(N_cut*f/fs)+1))+0.5*pi)
freq(round(N_cut*f/fs)+1)
结果离真实值就稍有偏差。这时，如果我们试试把fs提高到1000 Hz。
clear all;
fs = 1000;
t = 0:1/fs:9.2;
t=t(:);
f = 0.51
x = 2 * sin(2 * pi * f * t + 1);
N = length(x);
N_per_cycle = fs/f; % average points per cycle
N_cycles = floor(N / N_per_cycle); % maximum number of complete cycles
N_cut = round(N_cycles * N_per_cycle); % number of points for FFT
x_cut = x(1:N_cut);
Xraw = 2 * fft(x_cut) / N_cut;
Xraw = Xraw(1:ceil(N_cut/2));
freq = 0:fs/N_cut:fs/2-fs/N_cut;
A = abs(Xraw(round(N_cut*f/fs)+1))
delta = wrapTo2Pi(angle(Xraw(round(N_cut*f/fs)+1))+0.5*pi)
frq = freq(round(N_cut*f/fs)+1)
结果就比之前更接近真实值了。这说明，时域信号的采样频率越高，越有利于精确地重构。现在可以看一下重构的效果：
x_rec = A * sin(2*pi*frq*t+delta);
plot(t,x,'bo',t,x_rec,'r-') % Figure 10
Figure 10
下一篇文章会介绍当原时域信号的频率“不纯”的时候如何通过Fourier变换进行重构。