colloid | 万物皆流

在Google上搜东西，偶然进入了“台湾博硕士论文知识加值系统”，发现可能是由于我的IP没有购买什么权限之类，我的角色被诊断为“一般民众”。这应该相当于内地的“中国博士学位论文全文数据库”和“中国优秀硕士学位论文全文数据库”了吧。原来人家台湾对于硕士论文，“不优秀”的也收入全“国”库的。可能是人家人口少，也没搞扩招，所以硕士更少，不像我们，如果所有硕士都收库的话，任你多少个Dropbox云计算都能让中国人撑爆。我再插一句题外的，觉得中国人如果每个人都使用Dropbox，那就不存在什么云储存概念了。中国人就是喜欢拼命生孩子把自己的生活质量和人格生贱掉。在以前是不会贱掉的因为以前有门阀等级制度保证阶级固化。现在社会稍微平等一些，你人多人少就不一样了，所以就麻烦。中国的人口是多到反而适合用封建皇朝法统治的地步了。

所以回到刚才的话题就是说因为台湾硕士少所以它的“知识加值系统”可以把所有硕士的毕业论文都收库。我搜到的这位人兄名叫陈致中，跟陈水扁儿子同名。所以本文是标题党了一下。这位陈致中毕业时间是“96學年第2學期”，所以算是我的前辈了。它的硕士论文题目是“利用小角度X光散射探討稀薄二氧化矽/聚環氧乙烷懸浮液之作用力特色”，哎呀呀，台湾中文……“之作用力特色”……好文雅。从来不出现“的”，全部改成“之”。其摘要：

本研究藉由小角度X光散射（small angle X-ray scattering，簡稱SAXS）量測探討二氧化矽（silica）/聚環氧乙烷（poly(ethylene oxide)，簡稱PEO）懸浮液在不同PEO濃度下之結構與作用力特色。PEO會藉由氫鍵吸附在silica表面造成殼層結構（silica為實心球部份，PEO視為殼部份），造成立體障礙效應，影響膠體粒子間的立體作用力。本文利用殼層理論分析silica/PEO懸浮液的形狀因子（form factor），再運用等效硬球理論（equivalent hard-sphere potential model，簡稱EHS）、HPY理論（Hayer-Penfold/Yukawa potential model，簡稱HPY）、和方井理論（square-well potential model）探討silica/PEO懸浮液的結構因子（structure factor）。其中硬球理論和HPY理論都是探討溶液內部存在排斥力的情形，而方井理論為探討溶液內部為吸引力的情形。透過等效硬球理論、HPY、方井理論的分析可以得知silica/PEO懸浮液內立體排斥勢能（steric potential）、靜電勢能（electrostatic potentials）的相關重要性，瞭解主要作用力來源及溶液是否穩定。

从摘要来看是一项很经典的研究，虽然现在看来这种研究经典到都有点公式化了，但是在96年那会儿这种实验还是能强化一下理论的。经典体系（silica/PEO）经典手段（SAXS）经典结果（exp(U(h)/k_BT)之类）总是能让人百看不厌。

原来台湾把defend简单称为“口试”，不像我们称为“答辩”。我们的译法比较虚伪，好像还真的会要“辩”一下以体现科学精神似的，人家台湾就直接当成“考试”过关，辩什么辩？很坦白。我们叫“答辩委员”，人家也叫“口试委员”，不过我们叫做“答辩委员会主席”的，人家叫“召集委员”，没有什么“主席”。说明大陆学者想当官想疯了，学生答个辩的企么委员也要设立一个“主席”这种虚衔来过过官瘾啊官瘾。

摘要：溶解在胶体悬浮液中的聚合物，如果吸附在胶体粒子的表面，由于增加了斥力的作用距离，提高了粒子间作用势垒U_max，粒子聚集速率会降低。这是定性的解释。本实验既然能得到平移因子随聚合物浓度的变化关系，就想半定量地解释一下。聚合物吸附在粒子上的位阻势函数已经有成熟的理论模型。粒子聚集速率与作用势垒之间的关系也可以通过Smoluchowski方程和stability ratio来描述。难点在于说明两个关系：一是平移因子与U_max的关系，二是要从粒子的总势能函数U=U_范+U_电+U_聚合物的表达式求极大值，获得U_max与聚合物吸附量Γ或添加量c_p的关系。以下是我查阅资料后的总结，感觉没有能力再完善了。

1 Laponite的聚集速率

胶体粒子的聚集（coagulation）过程可分为扩散控制型和反应控制型。扩散控制型是由于粒子之间聚集反应十分快（活化能为零），因此反应速率基本只受制于碰撞机率。根据布朗运动的公式，可以写出其速率常数。而反应控制型则是由于粒子间成功地结合需要克服能垒U_max因而并非所有碰撞事件都能成功发生聚集，其速率常数就要比仅受扩散控制的k_D小。定义stability ratio，W = k_D / k_R，以表征反应难度（U_max）对聚集过程快慢的阻碍程度，则W应该跟U_max有关（以上可参见T. Cosgrove等合编的书[1]）。N. Fuch[2]定义，可用于从U(h)计算W，但U(r)的形式取决于具体的聚合物吸附模型（如Scheutjens–Fleer的平均场理论还是de Gennes的标度理论）且表达式复杂（因为还要加上范德华势和静电势），因此实际上往往直接采用W的近似式。例如S. Tawari等和A. Nelson等[3, 4]采用以下表达式来描述Laponite悬浮液的老化：

上式本来是Prieve and Ruckenstein[5]为球形粒子导出的近似表达式，Laponite作为非球状粒子，系数0.25应该偏大，但这一系数值的变化对W的大小影响很小（见S. Tawari等的讨论[3]），倒也可以不去修改。如果本文也采用此式，则有k_R ~ W^-1 ~ exp(-U_max/k_BT)。

根据Smoluchowski聚集理论的假设，聚集过程是一个二级反应控制聚集2A→P，产物生成量P随时间的变化关系是：

其中，A₀是反应物的量（作为粒子聚集体系就是初始粒子数），k是反应数率常数（即前文的k_R）。对于本文的体系，PEG的添加使得Laponite老化的过程被提前，就是由于聚合物的位阻作用，增大了U_max。而且U_max与PEG浓度c_p有关，因而数率常数k也与c_p有关。如果不同c_p下的曲线P(t_w, c_p)在时间尺度上有叠加性且平移因子为a_p(c_p)、叠加后主曲线的横坐标为t_w/a_p，那么就有k(c_p)/a_p = k₀（k₀为参考曲线的速率常数），即a_p ~ k^-1 ~ W ~ exp(U_max/k_BT)。这就是平移因子与U_max的关系。

Y. Joshi曾把Laponite老化叠加曲线的水平平移因子与exp(U_max/k_BT)相联系，但没有严格解释，只是一句带过[6]。

剩下的问题，就是U_max与c_p的关系。

2 Laponite的粒子间作用势

按照我想象，求U_max的方法就是去求U(h)函数的极大值，先求导再解方程。（不知道数学上是否有其他取巧的方法），因此要知道U(h)的具体形式。

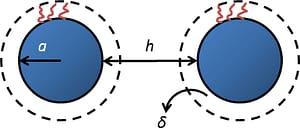
悬浮带电粒子间的作用势函数U(h)是指把两个粒子从距离无限远移动至距离为h所需要克服的能量。它可以看作是三个部分的加和：。静电相互作用（双电层）可采用U_DL(h) = C_DLexp(-κh)，其中C_DL为常数。该式适用于κ > 3的情况。范德华力可采用U_A(h) = –Aa/12h，其中A为Hamacker常数，a为样品的半径，该式适用于h << 2a。难点在于聚合物表面吸附之后的位阻作用势U_p(h)。

根据粒子间距h与聚合物层的厚度δ的关系，U_p(h)分为三段：1） h > 2δ, 此时U_p(h) = 0；2）δ < h < 2δ，此时两层聚合物重叠；3）0 < h < δ，此时聚合物层被压缩。

U_p(h)的计算方法一般分两步：第一步是统计聚合物链段在粒子表面邻近空间的分布；第二步是计算自由能。不同模型的区别主要在于第一步，其中Scheutjens-Fleer的格子理论（模仿Flory-Huggins的溶液理论在粒子表面之外划格子）和de Gennes的标度理论各有成功之处[1]。不管采用什么模型，以往研究都先给出平面的计算结果，再用Derjaguin近似推导球面的情况。也有嫌这两个理论都不完美，直接采用实验得到的分布（例如用SANS、ESR等方法）来代入到第二步进行计算。最近（2005）A. Lozs等给出了比较严格的计算结果（不用Derijaguin近似，直接计算重叠体积）[7]，表达式见下文。

对于本实验的Laponite体系，可以认为：1）离子强度较高（盐浓度高于CCC，见下文），忽略双电层的作用势；2）粒子间距范围在δ < h < 2δ，即吸附聚合物层作用不可忽略，但又不至于接近到被压缩。同时，根据SANS和DLS测量结果[4, 8]，也可认为δ << a，即h << 2a。因此，总势能函数如下：

，δ < h < 2δ << 2a

其中，c_ads是吸附在粒子表面的聚合物浓度，V₁是溶剂分子摩尔体积，ρ₂是聚合物密度，χ₁是聚合物与溶剂的相互作用参数，A是Hamacker常数。考察该式的重点在于聚合物浓度c_p的依速关系（体现为吸附量Γ）的依赖关系。该式第一项系数部分提示我们，U(h)与聚合物的表面吸附量的平方Γ²有关。式中所含的聚合物吸附层的厚度δ也于与吸附量Γ有关，Γ较小时δ随Γ增加缓慢（单层未吸附满）；Γ接近饱和时δ则随Γ迅速增加（打横吸附太挤，得改打竖）。实验上往往用从流力动力学半径得到的厚度δ_H来代入计算。T. Cosgrove曾介绍如何理论计算δ_H ~ Γ的关系[9]，大致上是要解Debye-Brinkman方程计算流场，结合既定的聚合物链段分布模型（如Scheutjens-Fleer模），找到流体动力学半径的边界。但是文章没有直接给出δ_H ~ Γ的表达式，只是给出计算机模拟的结果（求的是数值解）。我不懂按照T. Cosgrove[9]介绍的框架来自己推导表达式。

要对U(h, c_p)表达式求范围在δ_H < h < 2δ_H的极值——U_max(c_p)，才能知道U_max ~ c_p这层关系。所以目前整个理论探讨就卡在U(h, c_p)的具体形式上。假如这层关系知道了，那么整个a_p ~ k^-1 ~ W ~ U_max ~ c_p的关系就有一个比较完整的理论背景来讨论实验结果。我查了很多实验的文章（此略），δ_H ~ Γ曲线长得很像exponential关系。但即使认为δ_H ~ expΓ代入上面的U(h)表达式，对式子求导、解方程、求得U_max ~ c_p的任务也超出了我的数学能力。假如这一步没有别人帮助的话，目前文章的讨论只能说“本文实验获得了U_max ~ c_p定量关系”，至于这个关系理论上应该怎样，就没办法比较讨论了。

作此讨论的目的是为了说明本文的流变实验方法能够用于测量粒子相互作用能垒与各物理条件的定量关系。虽然DLS也常用于实现此目的，但由于涉及粒子尺寸多分散性的推导步骤一些近似处理，该方法只适用于聚集过程的早期（见下文）。而流变学的方法则是用整条聚集过程的曲线来叠加获得信息的，有优势。

3 临界凝聚浓度

上图是本论文另一个主要实验结果。不同盐浓度c_s下的主曲线进一步平移叠加而成的总主曲线。

所谓临界凝聚浓度（critical coagulation concentration，CCC）就是指W刚进入平台值区的临界盐浓度[1, 5]，盐浓度在CCC以上的体系静电斥力为零。与前文所述原因类似，盐浓度的平移因子直接跟stability ratio有关：a_s ~ W ~ c_s。因此小图里的实验结果就是典型的临界凝聚浓度的现象了[10-13]。CCC的位值与文献[14]结果相近（但可比性不强，因为该文献是用BaCl₂，CCC是与反离子价数有关的）。此结果说明c_s在4.5 mM以上，确实可以忽略静电斥力作用，支持了前文讨论的假设的合理性。而且上述结果说明，不同PEG浓度c_p的体系的CCC都出现在共同的位置，说明在粒子作用势当中，只要聚合物是非电解质，那么聚合物位阻作用部分和静电排斥作用部分确实是相互独立的（验证了一个常识）。

4 以往的类似实验工作

与静电排斥作用相比，通过非聚电解质聚合物吸附对胶体体系的稳定作用有不受离子强度影响的优点。要研究聚合物吸附对胶体体系的稳定作用，先要测量吸附量Γ与聚合物总浓度c_p的关系（其一），然后要测量胶体体系的凝聚过程（其二）。为了与相关的理论预测相比较，往往还需要测量聚合物吸附的表面体积分数分布φ(h)和粒子间作用势U(h)（其三）。以下介绍这三项任务的实验方法。

实验测量吸附量并获得吸附等温线的方法已为许多人所知，SANS、DLS、电泳、离心、NMR自旋弛豫等。这部内容太经典不详细回顾了。具体到本实验用的体系（Laponite/PEG）的吸附等温线也已有若干报道[8, 15-17]，大致呈Langmuire单层型的行为，但是这些实验的测量结果数据点偏少，结果可靠性令人怀疑。但是最有用的却是更早的一篇文章[18]，报道PEG在几种膨润土粒子上的吸附到达平衡的时间仅5 min左右（因此本实验结果已保证在平衡吸附下讨论），且吸附等温线能很好地由Freundlich关系描述：Γ ~ c_p^1/n（实验证据比较好），对本文参考价值较大。

要获得U(h)的信息，实验上可以通过SANS获得structure factor，再解Ornstein-Zernike积分方程来计算等效作用势，但这是间接的方法。直接测量U(h)的方法不多。平面与平面之间的方法是surface force apparatus（SFA），平面与粒子之间的方法是colloid探针原子力显微，真正直接测粒子与粒子之间作用势的只了解到有压缩Langmuir单层膜的方法（有参考文献，此略）。以上实验的结果都与已有理论进行拟合，总体来说S-F平均场理论和de Gennes标度理论各有成败。本文采用的U(h)模型（见上文）是基于S-F平均场的吸附链段空间分布推导出来的。

胶体的聚集过程则常常通过DLS监测平均扩散系数D随时间变化来观察，实验得到的D ~ t关系用Smoluchowski的预测相比较（拟合），可得到体系的反应速率常数k，进而得到W、U_max（最早报道建立此方法是文献[19, 20]）。以上方法基本成了此类实验研究的一种套路，只适用于聚合过程早期，且往往讨论到U_max为止，较少进一步联系U(h)的相关模型来讨论U_max与各种实验条件的关系（仅以我所查到的文献范围而论）。具体到本文的实验体系，A. Nelson等采用DLS的方法研究了Laponite/PEG的U_max ~ M_w关系[4]。本文采用流变学的方法根踪Laponite/PEG体系的聚集过程，并基于以上讨论，得到了U_max ~ c_p关系，以后可以用类似的方法研究更多不同的体系和物理条件。简单地说，“叠加曲线能够干嘛”是本文的卖点。这样也许比仅仅报道一个叠加现象档次要高些？