Tag Archives: gelation

凝胶化过程的松弛时间

前段时间，我花时间搞清楚了时温叠加（以及所有关于相关函数和响应函数的叠加）得到的松弛时间比值，是什么松弛时间。在KWW形式函数的情况，可证实叠加因子是平均松弛时间之比。最近这几天，我主要想搞清楚，凝胶化过程中的松弛时间是什么松弛时间。这里的凝胶化是指不可逆聚集（irreversible aggregation）过程中发生渝渗的凝胶化。

聚集导致的凝胶化，是粒子发生不可逆聚集（DLCA或RLCA机理）形成cluster，然后cluster之间聚集最后形成无限网络（或贯穿样品的网络）的过程。形成的cluster和网络都是分形。由cluster连接形成的网络还有很多洞，可借用玻璃的cage概念。剩余的自由cluster就被限制在cage里，它与其说要逃离cage扩散到外面去，不如说直接就加入到已有网络里去了。

在凝胶化点（渝渗点）之前是可以由Smoluchowski方程来描述的。假如做动态光散射，所谓松弛时间是用下式去拟合动态结构因子得到的：

f\left(q,t\right)=\exp\left(-q^2Dt\right)=\exp\left[-q^2\left(t/\tau\right)\right]
其中D=\frac{k_\textup{B}T}{6\pi\eta R_\textup{h}}所以τ正比于Rh。后者随时间的增长就是前者随时间的增长。凝胶化前期的聚集理论（Smoluchowski方程）就这么跟dynamics联系起来了

问题在于，凝胶化点之后怎么办。通过叠加得到的因子，应该仍是一个具有松弛时间概念的量。但是凝胶化之后体系的松弛时间发散了。叠加得到一个τ，又代表什么呢？我觉得这是剩余自由cluster从cage中逃离的平均时间。做动态光散射的时候，凝胶化之后的动态结构因子不能完全衰减，而是达到一个有限平台值，该值是Debye-Waller factor，又称为Edwards-Anderson order parameter。Krall等为了从这种形状的动态结构因子提取出一些结构信息，提出了一个模型，具体不详述了，其动态结构因子的表达式如下：

f\left(q,t\right)=\exp\left[ - \left( q \delta \right) ^2 \left( 1- \exp \left[ -\left( t / \tau \right) ^p \right] \right) \right]

所以，假如凝胶化之后相关函数或相应函数仍有什么叠加性，叠加因子就是上式这个τ的比值，而这个τ跟blob的尺寸R和弹性系数k有关。事实上，上式符合

f\left(q,t\right)=\exp\left(-q^2\left\langle\Delta r^2\right\rangle\right)

因此<Δr^2>就是cage的均方半径。τ跟<Δr^2>成反比，所以凝胶化点后τ的继续增长，反映的不是体系还能松弛，而是cage不断缩小，这是剩余自由cluster不断加入到主网络的结果。

最后重新强调一次概念性的问题，由于是“不可逆聚集”形成的凝胶（化学凝胶），所以凝胶化之后就动不了了，不存在有限松弛时间，这跟实际的物理凝胶不同。我们都知道，实际上的胶体凝胶都是物理凝胶，凝胶化点后可以谈论“一个很大的松弛时间”。但是，假如你想享受Smoluchowski方程的便利去描述凝胶化点之前的动力学，你相当于否定了体系是一个物理凝胶（对于吸引力较强的“强动力学体系”，确实也应该近似于化学凝胶），因此你不能又说凝胶化点后存在一个很大的松弛时间，至少你要承认体系已经绝对地nonergodic了。所以我才要借用Krall的理论，另外找一个动态结构来解释凝胶化点后得到的τ。

函数的平移叠加性是怎么来的？

最近写paper，所以基本上没时间在博客上长篇大论。倒是自从开通中文微博之后由于无需切换翻墙代理因此基本上长年挂在上面。现在如果你想挂微博，基本上什么客户端都有了。在所有各种手机，各种操作系统。但我发现，只有使用Chrome插件客户端之后我才真正利用了客户端实现长挂。这说明我的工作中心是Chrome浏览器。

WordPress升及到3.2之后也顺眼了N多，主要是Dashboard用的font family好像清理过了，该sans的sans、该serif的serif，就连monospaced的也很好看。在使用一段时间微博之后，发现这还是属于不假思索的人用的。所以基本上我还是会回归博客。

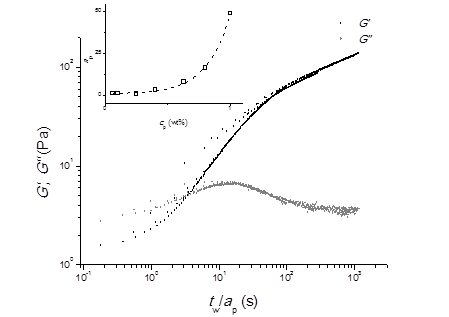
我的paper涉及到一个凝胶化过程的时间浓度叠加性，既不同浓度的体系凝胶化曲线（测的是模量曲线）log-log图可以通过水平平移叠加成一条主曲线的现象。我需要说明的是这时的平移因子就是凝胶化反应速率常数k。这好像本来是个显而易见的道理，但我发现一下子没办法清晰的说清楚，不得不查文献。渐渐发现以上事实的前提只需要是“单分子反应”即可。即只要是在谈论单分子反应，不管是几级反应。如果反应过程具有时间叠加性，那么平移因子就是速率常数。以下是通过简单的推导来展示这一事实。

Master curve and the shift factor

Master curve and the shift factor

一个n级单分子反应速率方程是：

\frac{d \left[ A \right]}{dt}=k\left[ A\right]^{n}

积分之后就是：

\begin{cases}& \left[A \right ]=\left[A\right]_{0}\exp\left(-kt\right),n=1\\ & \left[A \right ]=\left[\left(n-1 \right )kt+\left[A \right ]_{0}^{1-n}\right]^{\frac{1}{1-n}},n\neq1 \end{cases}

可见，速率方程总可以直接写成t'=kt的函数：\left[A\right]=f\left(t\right)=f\left(kt\right)。这时，如果k对某参量C（如浓度）有依赖性，并可以写成k=k_{0} a_{C}\left(C\right)，则有 f\left( kt /a_{C}\right)\equiv f\left(k_{0} t\right)，即f\left(t'/a_{C}\right) \equiv f\left(t_{0}'\right)。作成log-log图，则为\lg f\left(\lg t'-\lg a_{C}\right)\equiv\lg f\left(\lg t_{0}'\right)，即具有平移叠加等效性。

同理，关于结晶的过程有个Avrami方程X=\exp\left(-kt^n\right)。此时X能写成t'=kt^n的单值函数：X=X\left(t'\right)=\exp\left(-t'\right)。这时，如果结晶的速率常数k是温度的函数并可以写成：k=k_{0}a_{T}，那么就有f\left(t'/a_{T}\right) \equiv f\left(t_{0}'\right)、\lg f\left(\lg t'-\lg a_{T}\right) \equiv \lg f\left(\lg t_{0}'\right)，其log-log图同样具有平移叠加等效性。