最近我在找一些能描述应变硬化的粘弹性模型来模拟具有这种性质样品的LAOS的行为。找到很多以前用来描述橡胶拉伸的模型,它们都是纯弹性的。而我的样品有一定的迟滞,因此我就简单地给这些模型加上一个牛顿粘壶拉倒了。以下是一个小小的总结。
Tag Archives: laos
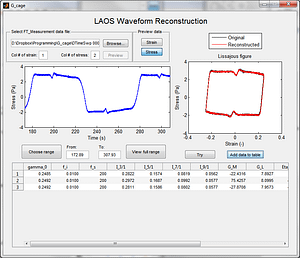
波形重构程序GUI
波形重构代码
对真实世界的信号进行求导,需要先大幅提高信号的信噪比,否则求导运算就是一个噪音放大器。对于LAOS实验的信号,由于假设其为一系列奇次谐波的和:![]() 。因此,可以据此直接进行波形重构。即通过FFT得到信号的谐波振幅和相位角,按照此式重构一个平滑的波型,再拿去做微分。原理很简单,但是在MATLAB里整了半天,强度是对的,但相位角永远是错的。研究了一晚上,才发现FFT得到的相位角总是少了90°,也不知道什么原因。总之加上这90°之后就完美了。为了减少日后摸索,把代码贴在这里:
。因此,可以据此直接进行波形重构。即通过FFT得到信号的谐波振幅和相位角,按照此式重构一个平滑的波型,再拿去做微分。原理很简单,但是在MATLAB里整了半天,强度是对的,但相位角永远是错的。研究了一晚上,才发现FFT得到的相位角总是少了90°,也不知道什么原因。总之加上这90°之后就完美了。为了减少日后摸索,把代码贴在这里:
clear all;close all;clc;
%============ Generate the signal for reconstruction ============%
fs=57; % sampling frequency
fi0=10/3; % input frequency
t=0:1/fs:123456/fs; % the length of signal is 12345.
t=t';
delta=[1 3 2 1];
x1=sin(2*pi*fi0*t); % the input signal is a sinusoidal wave;
x2=12*sin(2*pi*fi0*t+1) +3*sin(3*2*pi*fi0*t+3)+0.8*sin(5*2*pi*fi0*t+2)+0.02*sin(7*2*pi*fi0*t+1) +2*rand(size(t)); % the output is a sum of odd harmonics
x=[x1 x2];
%============ Reconstruction begins ============%
fi=sinfapm(x(:,1),fs); % the frequency is obtained by sinewave fitting.
Nr_cycles=floor(fi*length(x)/fs); % number of comlete cycles
N=round(Nr_cycles*fs/fi); % cutoff length for coherent sampling
x=x(1:N,:);
t=t(1:N); % cut the time axis too
Xraw=fft(x(:,2));
phase=angle(Xraw);
freq_bin=0:N-1; % frequency bin
freq_res=fs/N; % frequency resolution
freq_i=freq_bin*freq_res; % frequency axis
cutoff=ceil(N/2); % cut the first half of FFT
Xraw=2*Xraw(1:cutoff)/N;
phase=phase(1:cutoff);
max_nr_harm=7; % in practice the max number of harmonics is determined by the Nyquist frequency
I_n=zeros((max_nr_harm+1)/2,1); % amplitudes of the odd harmonics
delta_n=zeros((max_nr_harm+1)/2,1); % phase angles of the odd harmonics
% extract the harmonic information
for n=1:(max_nr_harm+1)/2
I_n(n)=abs(Xraw(round((2*n-1)*fi/freq_res)+1));
delta_n(n)=phase(round((2*n-1)*fi/freq_res)+1)+0.5*pi; % for the phase angles to be correct 0.5*pi must be added. The reason is unknown.
end
DC=abs(Xraw(1))*cos(angle(Xraw(1)))/2; % Normalization of the DC component need not multiply with 2, so the division by 2. The cosine factor determine the sign of DC offset.
fs2=300; % reconstruct the signal at a higher sampling frequency
t2=0:1/fs2:t(end);
t2=t2';
reconst=zeros(length(t2),2);
reconst(:,1)=sin(2*pi*fi*t2); % the input signal at high sampling frequency
% reconstruct the output signal by summing up the sine components
for n=1:2:max_nr_harm
reconst(:,2)=reconst(:,2)+I_n((n+1)/2)*sin(n*2*pi*fi*t2+delta_n((n+1)/2));
end
reconst(:,2)=reconst(:,2)+DC; % DC shift
plot(x(:,1),x(:,2),'k',reconst(:,1),reconst(:,2),'r')
为了展示,该代码生成一个示范信号。这个示范信号的频率、取样频率和长度都尽可能的任意(频率是个除不尽的小数,取样频率是个质数,长度是12345),也增加了比较明显的噪音。波形重构时,频率是通过对输入信号进行正弦波拟合来获得的。这一步对原信号的噪音还是十分敏感的。如果在以上代码给原信号加上高于千分之一的噪音,整个代码的结果就完全不及格了。这就要由于是后面决定谐波所处的frequency bin那步对信号频率的准确性十分敏感。
有了信号的频率,就可以进行相干取样、FFT……一切都按正常进行。
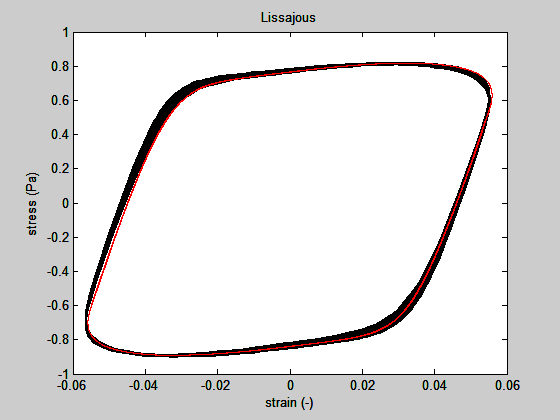
以上代码本身会给出一个结果比较。我用以上方法对一个真实的LAOS信号进行重构,得到的结果如下(黑的是实验结果,红的是重构曲线):