Tag Archives: nonlinear viscoelasticity

能描述延迟屈服的触变性模型

我的毕业论文打算有一节是使用一个触变性流变学模型来理解我的实验结果（谈不上拟合）。由于在这方面我是菜鸟，所以有些失败不知道是模型的问题还是我数学差推不出来的问题。其中一个就是屈服问题。

Glassy polymers和colloidal gels体系都有延迟屈服（delayed yielding）的现象。在做蠕变实验时，在中等大小的应力σ下，样品不是不屈服，但又不马上发生屈服，而是有一段延迟时间td。td跟施加应力σ的大小有关，σ足够大的话，就看不到延迟，td = 0；σ足够小的话，td趋于无穷，常规上讲法就是说施加应力小于样品的屈服应力σ < σy。所以，如果考虑延迟屈服现象的话，样品其实不存在一个特定的屈服应力σy作为屈服前后的界线；看不到屈服有可能只是观察时间不够长，但不代表样品内部没有事情在发生。这就麻烦大了。于是这段时间里到底发生了什么事，需要给个解释。

触变性流变学模型有几大类，具体可以看关于thixotropy的review。我采用的应该是比较简单的那一类，叫structural kinetic modal。就是把触变性流体看成一个含有结构参数λ的平衡态模型，而结构参数跟时间和剪切场有关，存在建立和破坏之间的竞争。有一大部分这类模型对这个结构参数的处理是仿效竞争反应动力学的做法，把它写成跟结构建立速率常数k1和破坏速率常数k2有关的一个速率方程。这样的模型自然是可以描述基本触变性现象，例如thixtropic loop和stress overshoot。但是，我在MATLAB里玩过几个这种模型，都没办法整出延迟屈服现象。屈服是有的，但是都是从t = 0开始发生，我能调的只是屈服过程的快慢，而不是何时开始发生。我没办法让它时长为td的时间内不发生任何事情，然后超过此时间之后再发生屈服。更谈不上调整td的长短了。

目前我怀疑如果要描述延迟屈服，光简单地用一个数值代进k1或k2是不够的。k1和k2需要进一步建模。不过，我必须想出一个idea到底延迟屈服的td时间内样品到底发生什么结构变化，能既不导致任何流变学现象，又控制着td的长短。

第四天交流@KIT

这天稍微闲了一些。由于昨天晚上看电影去了，所以今天上午的时间我主要在写昨天的日记。

Fritz-Haber-Weg

早上回institute的路上拍了一些路边植物的照片。我在广州没见过这些植物。另外，Fritz Haber曾经在Karlsruhe工作过，有条路就叫Fritz-Haber-Weg。

今天找了Johannes了解他的工作。已经发表了一篇文章在Macromol. Rapid Commun. 31:1337，用交联的丙烯酸水凝胶来进行海水淡化。水凝胶溶胀了海水之后，要通过机械挤压把水挤出来，挤出来的水会有一定程度的淡化。我是第一次听说水凝胶里的水能像海绵里的水那样挤出来的。想必能挤出来一点，但也把水凝胶挤烂了。而且也不希望结果是需要很大的力去挤（能耗问题）。所以水凝胶的力学性能（尤其是平衡溶胀时）是很重要的，需要具有软而韧的特点。而据我所知平衡溶胀时的水凝胶会很脆。（导师告诉我这是渗透压问题。因此就是渗透压和水凝胶的力学性能之间的关系问题了。）

能不能通过引入NIPAM单体来实现温度控制的收缩和溶胀循环？不行，因为要使水凝胶具有LCST性质，NIPAM的比例要很大，这就限制了丙烯酸单体的含量和离子交换的效率。也许通过一头是乙烯基，另一头是羧基的偶氮苯，可以实现光控的溶胀收缩，又不牺牲离子交换效率？但这是比较昂贵的合成。

下午五点半我正好要走的时候Prof. Whilhelm来找我，在他办公室聊了大概20分钟左右。我向他介绍了我的工作。他给了几个意见。一是关于In/1 ~ γ0平台值随n的变化关系问题，我的结果也许不必要用Brader的MCT预测，只需要简单的用一个剪切变稀的经验模型例如Carreau来预测就行了。二是关于Lissajous曲线的微分问题（获得McKinley的GM、GL参数），他建议不要直接做（哪怕数据已经进行了oversampling），而是仍然进行Fourier变换，取尽可能多次的高次谐波，重构Lissajous曲线，再去做微分，这能够降低微分的误差。令我印象深刻的是Prof. Whilhelm似乎脑中一起有挥之不去的“噪音”二字。他看任何东西都同时看到噪音。他看一个计算过程就是在看噪音在此过程中的走向，并随时相办法减小噪音。我本科的时候上普通物理实验课，头两节课就是讲有效数字、小数点等问题，误差分析问题。但是随后的实验课都没有遇到误差很大的情况，因为这些课程中的测量都经过设计，仪器也是很成熟的。等到我面对新的测量问题的时候，已经过去七、八年了。因此除非误差大到妨碍毕业，否则根本没有任何降噪的“追求”和“理想”，事实上导致有些该观察到的就观察不到，错失发现机会。

我还跟他谈到了我准备做LAOS时间扫描的想法，他没有太多的意见，但是提到说他之前也想过小波分析，但没做。

讨论当中他很不经意地说“Because you are a physicist…”，我就表示“flattered”，他问我难道不是physicist吗，我就告诉他我只有很weak的physical background，我本科学什么、master做什么，到了PhD才做流变学。但是我也和他讨论了很多mode coupling theory、流变学中的非平衡态问题、松弛时间尺度的问题等很物理的问题。我觉得如果光是吹牛，不用解方程，我还是基本可以被当做一个physicist的吧。一到要解方程我就歇菜了。

 

第三天交流@KIT

LAOS与percolation

今天上午又找Deepak聊天。他这两天都在用ARES-G2测量碳纳米管填充聚合物的样品。他使用8mm的cone-and-plate夹具。因此他要先把样品热压成8mm的薄片（190°C），然后再放到流变仪上用cone-and-plate继续压（也是190°C），直到上夹具达到所需的gap值。我留意到，ARES-G2的gap控制精度在小数点后五位！ARES只有2位。而且ARES-G2的升降也比ARES快。觉得当今位移控制的技术也太神奇了。

Deepak现在主要想考察percolation的问题。Deepak发现，向纯聚合物中添加碳纳米管，一开始I3/1是随添加浓度减小的，超过一定浓度之后I3/1才随碳纳米管的浓度增加而增加。Deepak很困惑为什么会有一段随着碳纳米管浓度增加而非线性粘弹性减小的区间，而在此区间里G’是不断增大的。

我也曾经尝试通过LAOS研究percolation问题，只是我的体系是PAA/Fe(III)凝胶，只能通过线性粘弹性的方法（Winter法）找percolation threshold。在LAOS条件下critical gel会不可逆破坏，看不到什么非线性粘弹性。

因此我的感觉是，仅仅形成网络结构并不意味着在LAOS下显示非线性粘弹性。后者需要所形成的网络具有可逆恢复的性质。而且恢复的松弛时间要跟LAOS的频率相耦合。不发生网络破坏，LAOS的波形就不会扭曲；不持续恢复和破坏，就得不到大量周期的非正弦LAOS结果（FFT之后就不出高次谐波）。

另外，我觉得就算在LAOS下样品显示出某种临界转变，转变点的位置也是不固定的，而是会依赖应变幅度。这个也许能算作percolation，但也跟Winter法的临界点没有可比性。总的来说我也觉得LAOS和SAOS的结果之间是没有可比性的。

跟Deepak还讨论了很多琐碎的问题，一个上午就过去了。

邀请报告

中午吃饭的时候又遇到了Madhi。我发现当其也人用德语聊天时候他总是很安静，加上他的名字，我就问他是来自哪里的，原来是伊朗。他在伊朗读博士学位，来德国这里交换六个月。他不经常说话但整天笑，很温文尔雅。

中午1点邀请了一个教授过来做报告，几乎全体组员都要参加，Prof. Whilhelm主持。报告者是Thomas Hanemann，来自Institute of Applied Materials，报告的题目是Polymer-based Materials in Microsystem Technologies。报告的主要内容放在微米级的光学元件上。对这种材料的要求首先是高透光率和高折射率。高透光率的聚合物有很多（例如PMMA等），但为了提高折射率，就要往聚合物里添加其他成份，往往就要降低透光率。提高折射率可以通过添加无机填料或者有机掺杂。无机填料产生的问题就是散射、分散性、浓度和表面性质等等都会影响材料的透光率。有机掺杂虽然没有散射的问题，但有很多分子本身又有颜色，而且掺了有机小分子对聚合物有增塑作用，降低了材料的力学稳定性（例如耐高温性质）。但这些都终归只是讨论，Prof. Hanemann还是成功地做出了一些材料。另外，Prof. Hanemann还在研究陶瓷的微量注塑技术（通过sol-gel方法）。这个技术可以用于做非常精细的元件。但是到了微量成形的尺度，各个环节都有难度。例如起始的feedstock需要优化，流道需要优化等等。

讲座大概花了一个小时，完了之后有Nico带Hanemann教授和他的学生参观实验室，然后又到一个房间里喝下午茶继续闲聊，各自介绍自己的工作内容，寻找合作。Hanemann有些学生是要研究feedstock的流体力学性质的，恰好Whilhelm的学生Roland就是专门捣鼓流动不稳定性的，于是还确实有合作的空间。

Fourier变换

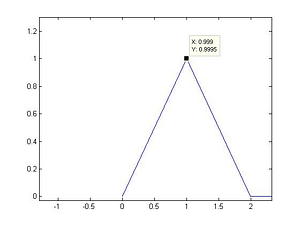
回到办公室已经是下午三点多了。我又请教Kathrin关于LAOS时间扫描的想法。由于我准备在一个长时间信号中逐段截取部分信号进行分析。因此截取的时间窗口的大小是受限的。如果在有限的时间窗口Δt中有N个数据（oversampling以后），那么Fourier变换之后的频率分辨率就是Δf = fs / N，fs是sampling frequency。进一步分析发现，Δf = f0 / Ncycle，f0是时域信号的频率，Ncycle是时域信号的周期数，必须是非零正整数。在给定f0的条件下，是不能既让Ncycle尽可能小又让Δf尽可能小的。如果情愿Ncycle尽可能小（Ncycle = 1）那么Δf = f0。也就是说Fourier变换之后的曲线就总是从f = 0一下跳到f = f0。应该是最差的情况。以下是f0 = 1Hz，Ncycle = 1的情况。

由于我是要取特定频率的幅值（f0、3f0、5f0……），我担心当Δf很大的时候，在所需的频率位置会没有数据点。但根据上面的分析只要Ncycle是非零正整数的话，这个情况是不会出现的。我又担心对于同样的时域信号，Fourier变换的Δf不同，得到的幅值会不同，至少当Δf特别低的时候。Kathrin倒是研究过这个问题，她给我看了一个结果，差别很小。因此也就不用担心这个问题。

频率分辨率的问题分析完之后，下一个问题就是实际信号的基频往往并不精确地等于实验输入的频率。例如我需要马达进行频率为1Hz的振荡，但实际马达信号取出来基频很可能是0.99Hz。这一点点差别在3f0、5f0等倍频处会成倍增大。如果我在做Fourier变换的时候以实验输入的（自以为是的）频率为基频来取谐波幅值，就有可能会出错。因此有必要先确定信号的真实基频，再进行Fourier变换。于是我请教确定信号的真实基频有没有比较“专业”一点的方法。讨论的结果是貌似没有，无非就是选择恰当的窗口进行find max。因此，先是为了确定基频就要占用一定的Ncycle。确定基频所用的Ncycle也是越小越好的。所以如果不确定上述的Δf太大对幅值没有影响，基频的确定这一步就很难保证了。

请教完Kathrin之后，我又拿同样的问题去请教Christopher。他顺便把他们做FT-Rheology的LabView软件拷了给我。跟Christopher的讨论就更详细了，他还提到如果我的应变幅度很小，Nyquist frequency又很高的话，高频的噪音很可能比基频还有大，find max必须（而不是最好）在合理的范围内。因此，软件界面还是需用户正确输入当初实验时的频率，以此作为基准左右开一个适当的窗口（何谓“恰当”可通过f0和Δf来确定）来find max。

Movie night

Käsespäkle

讨论完之后都快六点半了。晚上，Timo、Johanes等人叫我去地下室的一个cinema room那里看电影。我在Liftaß那里匆匆吃了晚饭，回旅馆洗了个澡。今天的晚餐是Kathrin推荐的菜谱之一：Käsespäkle。

就去cinema room。这个房间比较乱比较casual，有几张沙发，一张茶几，两台电脑，一个冰箱，还有各种散落电脑配件。中间空地上放了一个桌上足球。觉得是非常典型的西洋风格的休闲室。电影是二选一，一个是True Grit，一个是断背山。大家选了前者。他们都不喜欢字幕，也没字幕，所以全片都是浓重的美国西部口音和俚语也让我很受罪。我大概听懂个五六成，剩下的只能猜，不过也不影响剧情理解。边看边喝啤酒。我在国内都喜欢喝百威是因为嘉士伯喜力这些酒太浓。来德国这里喝的这种啤酒也是很浓的。看完电影之后，我提出让他们表演一下table football，结果人家技术确实不是盖的。这东西是不是跟斗地主在中国的地位一样呢——连斗地主都不懂简直就不是中国人。