3. 排版(typography)
英语的typography,释义是the visual components of the written words。前面提到的“语言风格”风格问题,都是独立于“视觉呈现”的。如果说“语言风格”是论文润色机构的任务,那么“视觉呈现”——排版——就是期刊出版社的任务。在当前的学术圈现状中,比起语言风格,作者在排版上需要承担的部分相对要少一些。但是,重视排版至少有以下必要性:
我经常碰到一些期刊审稿任务,稿子毫无排版可言,难以卒读。就算现在越来越多的杂志不对初稿的排版作要求,对初稿进行好的排版仍然有助于投稿成功率。
就算稿件正文的排版最终由期刊的出版社完成,稿件中的图、表范围内的风格和排版仍然属于作者自己决定的,除非原则问题否则出版社不会去改动
学术会议中的PPT和海报的排版问题仍然完全由研究人员自己管理
当然,本文默认的原则是,只要你愿意花钱,这些永远可以找专业的人去帮你做
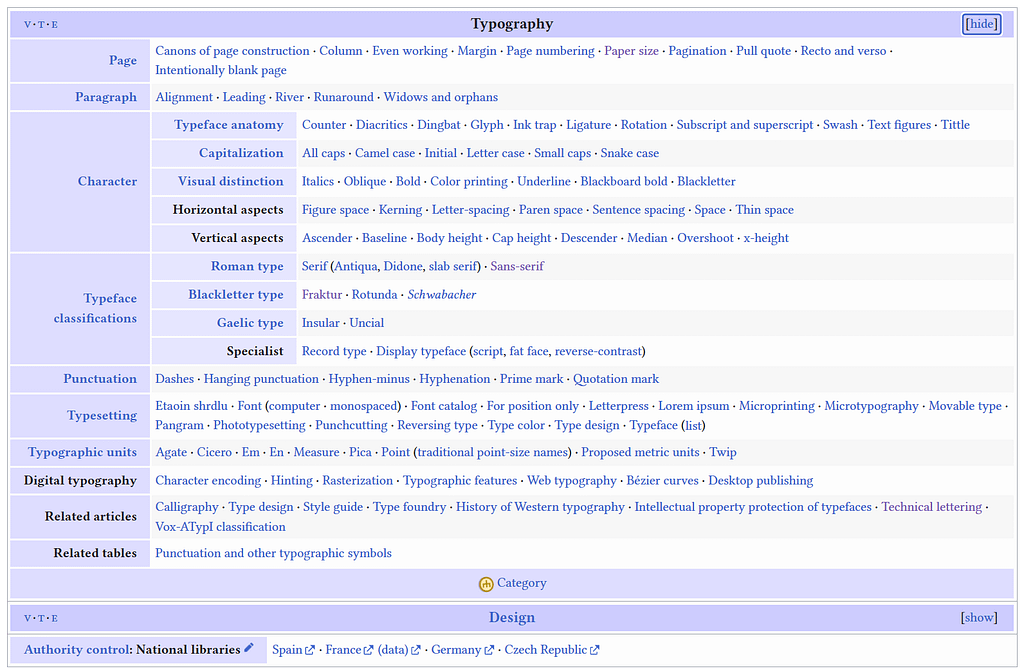
排版本身包括的知识很庞杂。下图是维基百科上typography词条 下的术语表,除了体现了排版知识的庞杂之外,倒是也按照按照对象的空间尺度分了类——这也是我们入手任何排版任务时应该考虑的顺序:页面设置、段落、字符和标点符号。
维基百科上typograpy词条下的术语表。注意page、paragraph、character和puctuation四个层次。
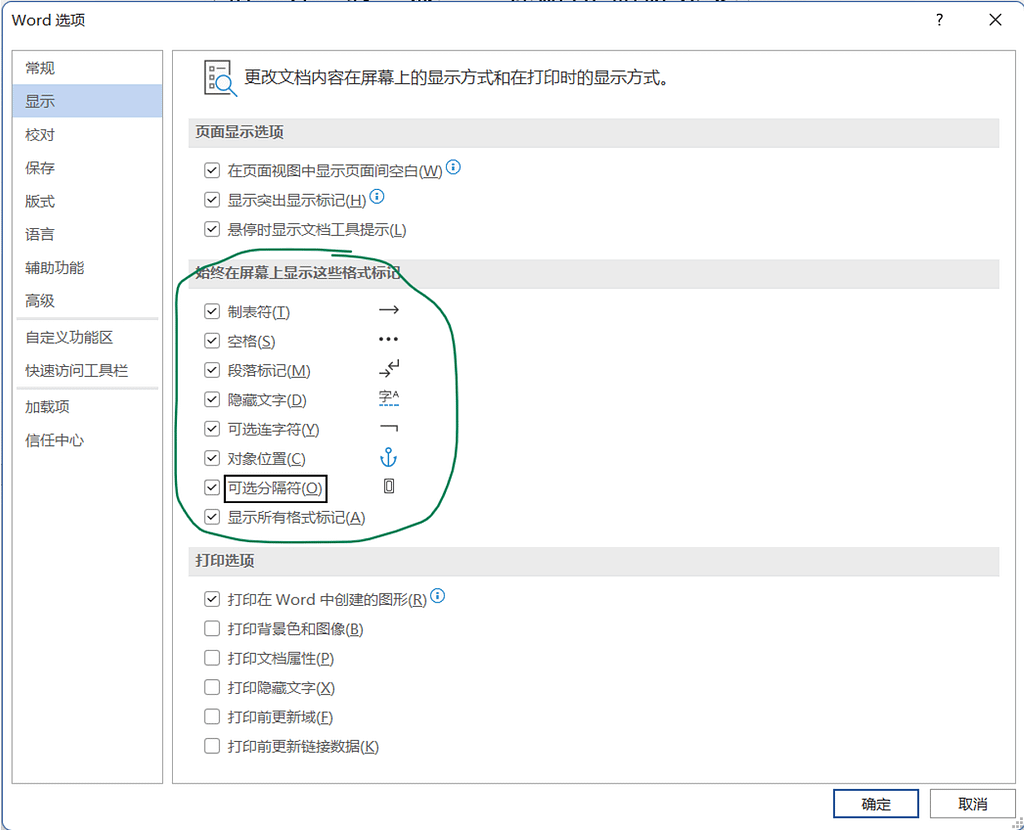
首先,在Word中,设置显示回车、空格等非印刷字符,将有助于我们排版。
建议在Word中设置显示所有格式标记。
标点符号的一些问题,我在前面已经讲过了。以下我将从小到大,按字符(characters)、段落(paragraphs)到页面(pages)的顺序讲。
3.1 字符
在Word中这对应着“字符”设置对话框。
在字符方面我们首先要区分两类英文字体家族:衬线字体(serif)和无衬线字体(sans serif)。衬线字体的一些修饰特征,使得我们可以更快的阅读更小、更密集的文字。因为我们的眼睛只需扫过这些修饰之处,而无须完整辨认出整个字母,我们的大脑就能帮我们“脑补”出整个字母。反之,无衬线字体多多少少需要我们更加定睛去看清每一个字母。所以,衬线字体更适用于大量文字的正文。无衬线字体适用于标题(包括小标题)或者字少的屏幕显示(比如讲演幻灯片)。不过,我认为这里面没有特别严格的原则性规定。我建议各位多翻阅优雅的出版物,找到自己喜欢的方式。按照上述的应用理由,在中文里,宋体可属于衬线字体,黑体和各类等线体可属于无衬线字体,因为它们也具有上述的效应。但是,我个人品味喜欢使用一种合适的楷体来作为正文字体,关于使用楷体的体会我会在整个系列文章的最后分享。
衬线字体(serif)和无衬线字体(sans serif)的主要区别
其次我们要注意英语中的“斜体”分为italic和slanted。slanted意思就是生硬的把正体字拉斜,而不作任何改动。slanted是不常见的做法,但我在这里提出是有原因的,马上会详述。
Italic和slanted对同一字体的不同处理
事实上,一个字体集(font family)的不同的风格(typeface)都需要独立设计,也以独立的字体文件形式存在。例如,如果某名称的字体,事实上没有提供italic的设计,那这一字体就没有斜体。上图给出了一个字体的italic处理,我们从字母a、f、n、i、v等的区别就容易理解为什么“斜体是需要独立设计的字体文件”,而如果你真的只需要slanted,根本无需设计师去独立设计,只需要计算机自动把原本的正体字仿射地拉斜即可。严格来说,“粗体”(bold)只是使用了某个较大字重(font weight)的版本而已。一个比较齐全字体集还可以提供更多不同字重,往往从bold,semibold,……一直到light。但“加粗”也同样是可以通过仅从一套常规字重的字体通过计算自动实现的。
很不幸地,Word默认提供这些功能。既倘若你所选定字体没有粗体或者italic的设计,在Word中仍然能设置斜体和粗体,这时Word给出的斜体就只是slanted。
特别地,中文字体都没有“斜体”一说。如果你在Word里对中文字体设置“斜体”,你看到的就是slanted的结果。
在这里我要解释两个问题。一是:slanted不好吗?二是:中文字体为什么没有“斜体”一说。
Slanted跟Italic相比的“不好”可以这么去理解。在古腾堡印刷传统中,当人们需要使用一种不同的风格时,往往是有一定的表意目的。比如,在英语中为了强调(emphasize),所以要用斜体。为了表示书名或者文章的标题,需要使用斜体。在英文印刷的历史长河中,斜体字母都是要另外刻的,没有计算机帮你把印出来的正体拉成斜体。那么,旧时代的字体设计师门既然要给同一字体集设计一套斜体,为何不干脆把每个正体拉斜了事,而是要像上图例子那般给一些字母换一种设计呢?这个问题我只需提出,答案大家可以自己查阅。但既有这一问,就说明我们在正式表意目标下需要使用斜体时,应该使用的就是italic。
但是上面说slanted的“不好”是加了引号的,因为这不是绝对地在所有场合都不受欢迎。我们注意到,上图中的例子是衬线字体。对于非衬线字体,本来就没有这些修饰,因此它的斜体就往往难说有什么重新设计的原则(除非设计师有它自己的美学意图)。下图是又一个例子。
Italic对于无衬线字体,很可能本来就是一个slanted的效果。 从上图的Impact字体可以感受到,我们也许在设计广告牌之类需要使用艺术字的时候,将享有更自由的做法,此时完全没必要排除slanted在任何一个字体集的可能,只要这在艺术上精准体现了你的意图。学术场合中,也许只要制作讲演幻灯片或海报的时候,才会有这种因素。正式文本需要按正式文书惯例。
文字体为什么“没有斜体”,这里相关的判断也是加了引号的。主张中文“没有斜体”的,讨论范围仅限于“斜体在英文文章中的用法”这一对比上。比如,中文不用斜体来表强调,而是用重点号。中文也不用斜体来表示书名或者文章的标题,而是使用中文的书名号“《》”(我们课题组的要求中,不采用方引号)。还有,中文在进行成段的引用(对应于英文中的block quote)时,也不会采用斜体。重点号可方便地在Word和Latex的CTeX环境下实现,但它很难在更多富文本编辑框中实现,所以也可以接受采用其他方式来实现,例如加粗,或者换一种字体集或字体风格,总之用回避slanted效果的斜体来实现上述的目的,主要批评的是那种照版英文原文的style到中文翻译上的做法。但是,也需要注意的是,中文规范中也并非完全不采用斜体。正如我在对slanted的解释里说的道理,在展示用途中,作为“艺术字”的功能,没有完全排斥slanted的原则。这个知乎回答 中举的中文斜体应用例子,正是由于它讨论的是展示用途,而非要在中文正文中表示强调等。
我在这里抛出一个原则:同一文本,不要使用超过两种风格的字体。这里的“风格”是泛指上述各层面:不要有两种serif或者两种san serif、不要有两种字体集、不要有两种字重……等等。“不超过两种”原则限制,能严格遵守,就严格遵守。大家也可以翻阅大量学术文献的出版版本或者学术专著的印刷版来体会它们是否违反了我在此抛出的原则。
字符层面需要调节的尺度,包括字母间距和单词间距。下图展示了这个问题下不同做法的效果。当然,一般情况下,Word帮你把这件事按默认设置处理好。但这不代表默认设置在任何情况下都是最好看的。我在这里举一个例子:中文的字符间距,往往需要跟据行距、段落和页面的情况进行调节,默认间距往往相对过密。但是,我一时很难找到漂亮的正面例子来说明这个问题,以后碰到了,会补进来。
英文的字母间距调整还会涉及到kerning和ligature问题(如下图),在这里只是提示大家留意这些现象,但未必是你需要亲自注意的,因为这些问题在专业的编辑软件中都帮你解决好了。
Ligature现象 Kerning现象
上下标的字到底缩到正常字的百分之几大小,放在正常字的多高或多低的水平位置,原则上都是可调的。但一般情况Word已有的默认设置我们不去改动。这件事在公式问题上可能更有实际意义些。
Mathtype中的上、下标设置
3.2 段落
Word中的“段落”设置对话框中的内容,代表了排版中关于段落层次需要考虑的绝大部分问题。
全英文稿避免两端对齐。
现在很多期刊论文都是双栏甚至三栏排版的。之所以有这种偏好,是认为一行的单词数超过某值时会造成阅读困难,而普通印刷品的纸张大小(A4或Letter)又有那么宽,所以分栏。分栏后往往使得一行放不下几个单词,特别是当长单词比较多的时候。
这时如果我们坚持采用两端对齐(justification),就会出现下图的不良情况:1)出现“河流”(river);2)词间距无法统一;3)甚至字符间距也无法统一。所以,左对齐(让右侧参次不齐不去管)是推荐做法。
两端对齐(justification)造成的各种问题。 有人问了,长的单词,用连字号来断开不好吗?确实也有一个设计原则不鼓励使用连字号把一个长单词断开成两截。但我认为这不失为一个权宜之计,特别是在中英混排不得不采用两端对齐的情况下,允许长英文单词以连字号断开是最佳的做法。
句与句之间,是有着与单词之间不一样大小的间隔的。在纸媒印刷的时代,人们可以自由创建任意大小的间隔,但是在打字机时期,我们只能按键盘上的空格键若干次,成倍地制造间隔。因此,在打字机时期形成了一种惯例,句中的标点符号(如逗号、分号、引号)后只打1个空格——这是单词间距,但是句末的标点符号(如句号、感叹号、问号)后要打2个空格。下图是打字机时代的一个例子。可以看出,若不是这么做,人在阅读时很难留意到句末。英语水平有限的同学可能体会不深,如果你希望迅速阅读一篇文章,准备使用“一目十行”的技能时,迅速判断语法结构是关键。而判断完整句子的结束与否,在英语语法中也是一个重要的要求。打字机时代之所以需要让句子间隔夸张起来,是因为打字机无法做到kerning,且每个字母的大小又是相同的。
在这个极端的例子中,句点后打了3个空格。
这是Word时代仍然延用不当传统造成的后果,结合“两端对齐”后,多余的空格给段落造成了大量的“河流”。
事实上在印刷业,使用单词间隔的2倍作为句子间隔是过于夸张了。所以,业界很早就明确规定:句末标点后,也按一次空格。到了Word时代的今天,很多排版问题Word都通过算法和默认设置自动解决了,但为了用户的传统,又保留了很多打字机时代的操作方式。例如,Word完全可以取消标点符号后打一个空格键的要求,因为算法完全能判断出标点符号的类型,并自动加上排版上所需大小的相应间隔。但这严重违返了打字机时代的惯例。这就好比至今“保存”按钮的图标是早已消失的物品:3.5英寸磁盘。正是因为排版学和排版软件的现状充满了类似这般理论上的“不自洽”,使得我们常常想要深究时都处处碰壁,思想更加混乱。我能啰嗦就啰嗦,但更多时候需要大家对排版学本身感兴趣,多了解其历史,来得到缓解。
我们更经常要求调节的是“行距”。这个概念也是笼统的。严格意义上,类似“行距”意义的,有好几个概念,如下图所示。在Word当中的“行距”设置,调节的是下图中的line space。而在Windows系统下的Word软件,调用不同字体时,可能由于字体的内部设计,“行高”(下图的line height)会有冗余空白(既远超ascent、descent的多余行高),叠加到Word的行距设置上,使得行距设置值相同,但采用了不同字体时,印刷效果上的实际行距不同。给你带来这种困扰的字体应该永久性拉黑。
前面提到,分栏的目的是减少每行的单词数。但是分栏后的栏宽受与页面大小和分栏数有关,字体本身的大小则是另一个独立的设置。你首先需要满足的原则是每行的单词数,具体怎么分栏,则要根据你字号来定。每行的单词数,叫the measure。有说法称,一行最好大概只有7到10个单词,供大家参考。
正式排版中我们还要避免“孤儿”(orphan)和“寡妇”(widow),下图是寡妇的例子:一个段落的最后一行成了某页的第一行。相应地,孤儿则是指一个段落的第一行成了某页的最后一行。我们当然希望,一个完整段落处于同一页,这样我们如果在段落内需要重读的时候不需要来回翻页造成心情烦躁。但书稿总之是要分页的,很难要求段落不被分页断开,因此我们至少希望不要造成孤儿或者寡妇。
寡妇(widow):一个段落的最后一行成了某页的第一行。 3.3 页面
Word中“页面设置”对话框中的内容,代表了排版中“页面”层次需要注意的大部分问题。我暂时想不到有什么特别值得在这里说的事情。
3.4 排版中的长度单位
磅(point)是出版用的单位体系,在这一单位体系12进制的,可能较常碰到的还有pica,12 picas = 1 points。在今天出版单位体系表示的各类尺寸,已经跟真实世界的物理尺寸建立了联系:1 inch = 72 points。
磅和英寸的换算关系
在屏幕显示方面,还会涉及到物理尺寸与像素之间的对应关系问题。例如,在一些专业作图软件中,字号既可表示为磅,又可表示为像素。但前者是使打印出来的东西的一致性所应采用的单位(因为它是物理长度单位,跟厘米英寸一样),但像素则是为了使屏幕显示出来的东西有一致性(看你怎么定义一致性)所应采用的单位。因为屏幕的最小显示元素是像素,无法在小于1像素之内做什么文章。所以在低分辨屏时代大家很精确地计算像素,因而习惯了像素单位。磅和像素之间的换算是一笔乱帐。大部分软件可能是按照1 inch = 96 px的惯例,来决定你设定了多少磅或多少英寸的东西,在显示屏上以多少像素显示给你看。你心里应该清楚,你不是在做网页设计或者软件界面设计,你的目标是打印出来之后的结果,所以软件的屏幕显示给你看到的只是“预览”。你应该抓住不放的是物理长度尺寸。
总之,“磅”在今天变成了无非是又一个物理长度单位。在排版时,处理各类物理长度单位之间的换算是家常便饭,建议在一旁打开计算器的长度换算功能。
在Word中文版当中,我们会碰到“字符”的单位,它不是一个物理长度单位。无论你用多大的字号(用物理长度单位表示,如多少磅),1字符都是指一个中文字的宽度。所以它是一个相对单位。英文中类似的单位是em和en,它们分别对应一个大写字母M和一个大写字母N的宽度。纵向维度类似的单位还有x-height,但它在word设置中用不上。
3.5 The HATS
HATS(Headings, Access, Typography, Spacing)代表着四个排版时需要注意的方面。后面两个跟前文介绍的内容有所重合。
Heading就是指,你写文章的时候要注意用小标题分节,不要哗啦啦从头写到尾。同时,提供一个小标题的目录。
Access是指,使用项目列表、表格、图形和照片来增加你文章的易读性。
Spacing方面,除了前文提到的各种排版中的常规间距问题外,还需要注意通过间距设置来产生对比,抓住或引领读者的眼球。这在一些宣传册、海报或者讲演PPT的设计中是有实用性的。
Z字形安排的内容顺序,更符合大部分人的阅读习惯。图中的方向是以从左到右(LTR)语言为例的。
3.6 中英混排的问题
至今中英混排的排版原则仍然没有特别完善。所以我对同学们的建议还是严格遵守学校发布的《学位论文撰写规范》以及里面提到的国家规定来进行中英混排。
Word已经在这件事上做了很多事情。但我们仍需注意的是:
左对齐还是两端对齐?如何表示中文的强调?中文标点符号的kerning?英文单词与中文之间的空隙?
所谓“中文标点符号的kerning”是指什么?例如:小明说:“今天天气真好!”在这里,冒号和左双引号同占一个中文字符空间,感叹号与右双引号同占一个中文字符空间。事实上Word的默认设置自动帮你做了这件事,但是在PowerPoint的文本框中这不是默认设置,你需要进设置使“中文版式”生效。
Word在中英混排时的部分自动处理。 如果你对中英混排的排版原则感兴趣,最好首先搜索相关设计领域的专业文章来作初步了解,然后做一下大陆和港台地区的不同官方规定的调查比较(甚至扩展到日文的规定),再去形成自己的理解。我这里留两个链接: